Scalar Projection, Vector Projection, Scalar Rejection and Vector Rejection
Definitions based on angle $\theta$
(1)标量投影(Scalar projection)1
向量$\boldsymbol{a}$对向量$\boldsymbol{b}$的标量投影定义为:
\[a_1=\vert\vert\boldsymbol{a}\vert\vert\cos\theta\]其中$\theta$为向量$\boldsymbol{a}$和向量$\boldsymbol{b}$之间的夹角。
(2)向量投影(Vector projection)
向量$\boldsymbol{a}$对向量$\boldsymbol{b}$的向量投影定义为:
\[\boldsymbol{a}_1=a_1\hat{\boldsymbol{b}}=(\vert\vert\boldsymbol{a}\vert\vert\cos\theta)\hat{\boldsymbol{b}}\]其中,$\hat{\boldsymbol{b}}$是与向量$\boldsymbol{b}$同方向的单位向量。可以看到,标量投影是相应的向量投影的模长。
(3)Vector rejection
向量$\boldsymbol{a}$对向量$\boldsymbol{b}$的Vector rejection定义为:
\[\begin{split} \boldsymbol{a}_2&=\boldsymbol{a}-\boldsymbol{a}_1\\ &=\boldsymbol{a}-(\vert\vert\boldsymbol{a}\vert\vert\cos\theta)\hat{\boldsymbol{b}} \end{split}\](4)Scalar rejection
同样地,Scalar rejection定义为Vector rejection的模长:
\[a_2=\vert\vert\boldsymbol{a}_2\vert\vert\]并且从几何的角度可以很容易地推导出:
\[a_2=\vert\vert\boldsymbol{a}\vert\vert\sin\theta\]Definitions in terms of $\boldsymbol{a}$ and $\boldsymbol{b}$
在有些情况下,角度$\theta$未知,我们需要基于向量$\boldsymbol{a}$和向量$\boldsymbol{b}$的计算出角度$\theta$(根据点积的定义 2):
\[\cos\theta=\dfrac{\langle\boldsymbol{a},\boldsymbol{b}\rangle}{\vert\vert\boldsymbol{a}\vert\vert\ \vert\vert\boldsymbol{b}\vert\vert}\]因此,直接基于向量$\boldsymbol{a}$和向量$\boldsymbol{b}$定义上述四个量是更加方便的。
(1)标量投影(Scalar projection)
\[a_1=\vert\vert\boldsymbol{a}\vert\vert\cos\theta=\dfrac{\langle\boldsymbol{a},\boldsymbol{b}\rangle}{\vert\vert\boldsymbol{b}\vert\vert}\](2)向量投影(Vector projection)
\[\boldsymbol{a}_1=a_1\hat{\boldsymbol{b}}=\dfrac{\langle\boldsymbol{a},\boldsymbol{b}\rangle}{\vert\vert\boldsymbol{b}\vert\vert}\dfrac{\boldsymbol{b}}{\vert\vert\boldsymbol{b}\vert\vert}\]等价于:
\[\boldsymbol{a}_1=\langle\boldsymbol{a},\hat{\boldsymbol{b}}\rangle\hat{\boldsymbol{b}}\]或者:
\[\boldsymbol{a}_1=\dfrac{\langle\boldsymbol{a},\boldsymbol{b}\rangle}{\vert\vert\boldsymbol{b}\vert\vert^2}\boldsymbol{b}=\dfrac{\langle\boldsymbol{a},\boldsymbol{b}\rangle}{\langle\boldsymbol{b},\boldsymbol{b}\rangle}\boldsymbol{b}\](3)Scalar rejection
记向量$\boldsymbol{b}=(b_x,b_y)$的正交向量为$\boldsymbol{b}^\perp=(-b_y,b_x)$,则Scalar rejection可以写作:
\[a_2 =\vert\vert\boldsymbol{a}\vert\vert\sin\theta =\vert\vert\boldsymbol{a}\vert\vert\dfrac{\langle\boldsymbol{a},\boldsymbol{b}^\perp\rangle}{\vert\vert\boldsymbol{a}\vert\vert\ \vert\vert\boldsymbol{b}^\perp\vert\vert} =\dfrac{\langle\boldsymbol{a},\boldsymbol{b}^\perp\rangle}{\vert\vert\boldsymbol{b}\vert\vert}\]其中,点积$\boldsymbol{a}\cdot\boldsymbol{b}^\perp$也被称作垂直点积(perp dot product)。
(4)Vector rejection \(\begin{split} \boldsymbol{a}_2&=\boldsymbol{a}-\boldsymbol{a}_1\\ &=\boldsymbol{a}-\dfrac{\langle\boldsymbol{a},\boldsymbol{b}\rangle}{\langle\boldsymbol{b},\boldsymbol{b}\rangle}\boldsymbol{b} \end{split}\)
Added on Nov. 2, 2023: The notions of vector projection and vector rejection are used in Gram-Schmidt Process, which could be found in 3.
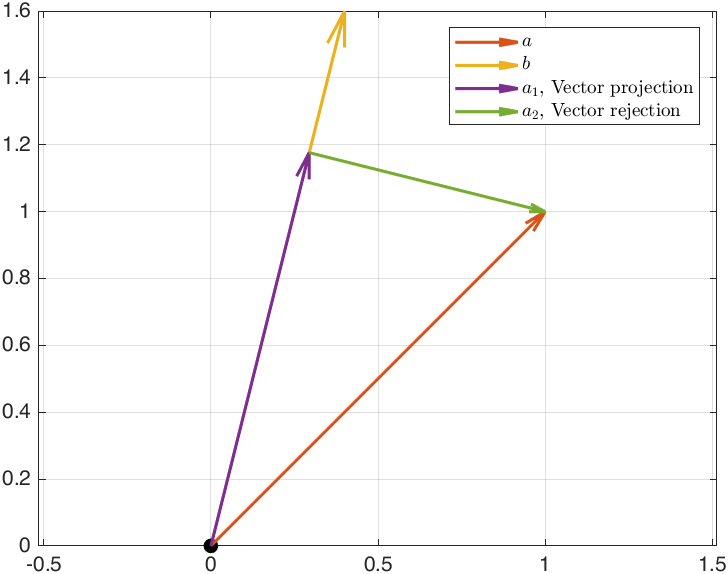
基于向量$\boldsymbol{a}$和向量$\boldsymbol{b}$的定义在编程时更方便计算。以向量$\boldsymbol{a}=(1,1)$,$\boldsymbol{b}=(0.4,1.6)$进行验证:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
clc,clear,close all
hold(gca,"on")
box(gca,"on")
grid(gca,"on")
axis(gca,"equal")
vecA = [1,1];
vecB = [0.4,1.6];
vecA1 = (vecA*vecB')/(vecB*vecB')*vecB;
vecA2 = vecA-(vecA*vecB')/(vecB*vecB')*vecB;
scatter3(0,0,0,50, ...
'filled','o','MarkerFaceColor','k','HandleVisibility','off')
q1 = quiver(0,0,vecA(1),vecA(2), ...
'LineWidth',1.5,'AutoScale','off','DisplayName','$a$');
q2 = quiver(0,0,vecB(1),vecB(2), ...
'LineWidth',1.5,'AutoScale','off','DisplayName','$b$');
q3 = quiver(0,0,vecA1(1),vecA1(2), ...
'LineWidth',1.5,'AutoScale','off','DisplayName','$a_1$, Vector projection');
q4 = quiver(vecA1(1),vecA1(2),vecA2(1),vecA2(2), ...
'LineWidth',1.5,'AutoScale','off','DisplayName','$a_2$, Vector rejection');
legend('Interpreter','latex')
References