The $\alpha$-sublevel Set of Convex Function
The $\alpha$-sublevel set of convex function is defined as1:
Convex functions2 give rise to a particularly important type of convex set called an $\alpha$-sublevel set. Given a convex function $f:\mathbb{R}^n\rightarrow\mathbb{R}$ and a real number $\alpha\in\mathbb{R}$, the $\alpha$-sublevel set is defined as:
\[C_{\alpha}=\{\boldsymbol{\mathrm{x}}\in\mathscr{D}(f):f(\boldsymbol{\mathrm{x}})\le\alpha\}\notag\]In other words, the $\alpha$-sublevel set is the set of ALL points $\boldsymbol{\mathrm{x}}$ such that $f(\boldsymbol{\mathrm{x}})\le\alpha$.
Due to the fact that $f$ is a convex function, now consider $\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\in C_\alpha$ (hence also $\boldsymbol{\mathrm{x}},\boldsymbol{\mathrm{y}}\in\mathscr{D}(f)$) such that $f(\boldsymbol{\mathrm{x}})\le\alpha$ and $f(\boldsymbol{\mathrm{y}})\le\alpha$, for $0\le\theta\le1$ we have :
\[f(\theta\boldsymbol{\boldsymbol{\mathrm{x}}}+(1-\theta)\boldsymbol{\boldsymbol{\mathrm{y}}})\le\theta f(\boldsymbol{\boldsymbol{\mathrm{x}}})+(1-\theta)f(\boldsymbol{\boldsymbol{\mathrm{y}}})\le\theta\alpha+(1-\theta)\alpha=\alpha\notag\]i.e.
\[f(\theta\boldsymbol{\boldsymbol{\mathrm{x}}}+(1-\theta)\boldsymbol{\boldsymbol{\mathrm{y}}})\le\alpha\notag\]which means that
\[\theta\boldsymbol{\boldsymbol{\mathrm{x}}}+(1-\theta)\boldsymbol{\mathrm{y}}\in C_\alpha\notag\]In conclusion, $\boldsymbol{\mathrm{x}}$ and $\boldsymbol{\mathrm{y}}$ belong to $C_\alpha$, and $(\theta\boldsymbol{\boldsymbol{\mathrm{x}}}+(1-\theta)\boldsymbol{\mathrm{y}})$ also belongs to $C_\alpha$, so $C_\alpha$ is a convex set3. To put it more concisely, “the $\alpha$-sublevel set of a convex function is convex”. Here is a one-dimensional case4.
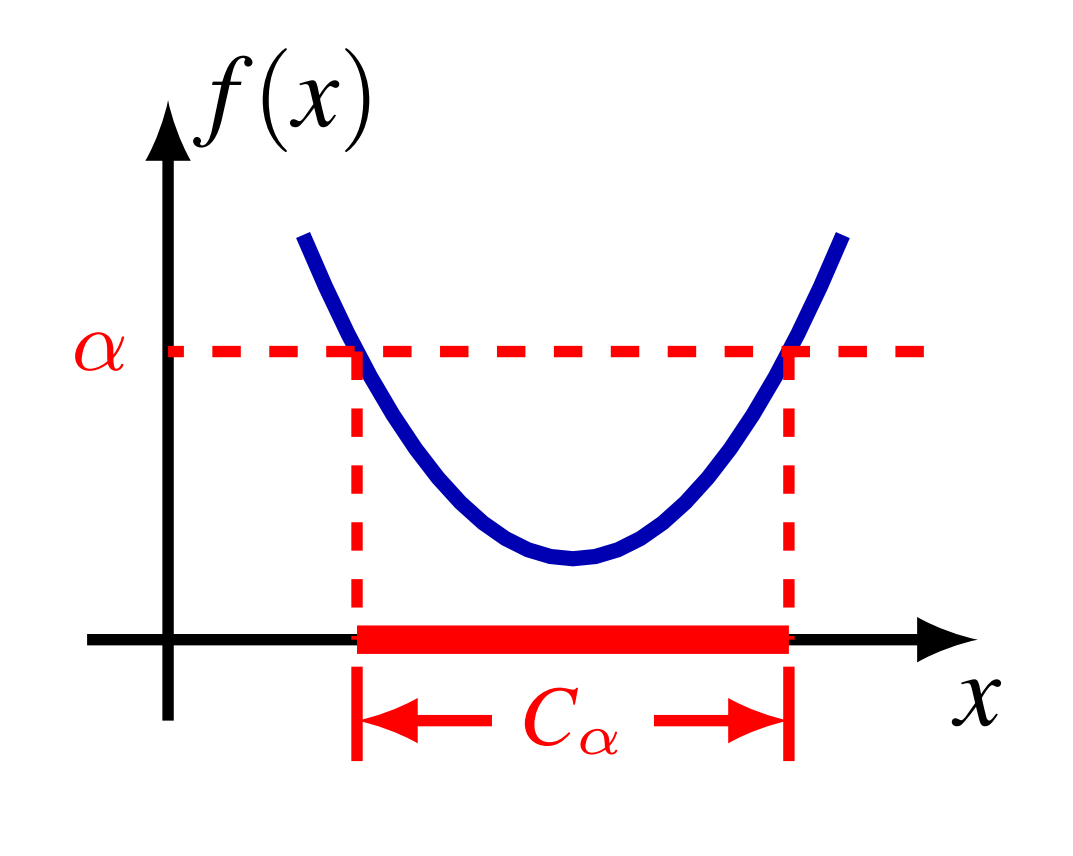
And on the other hand, non-convex functions can also have convex $\alpha$-sublevel sets4:
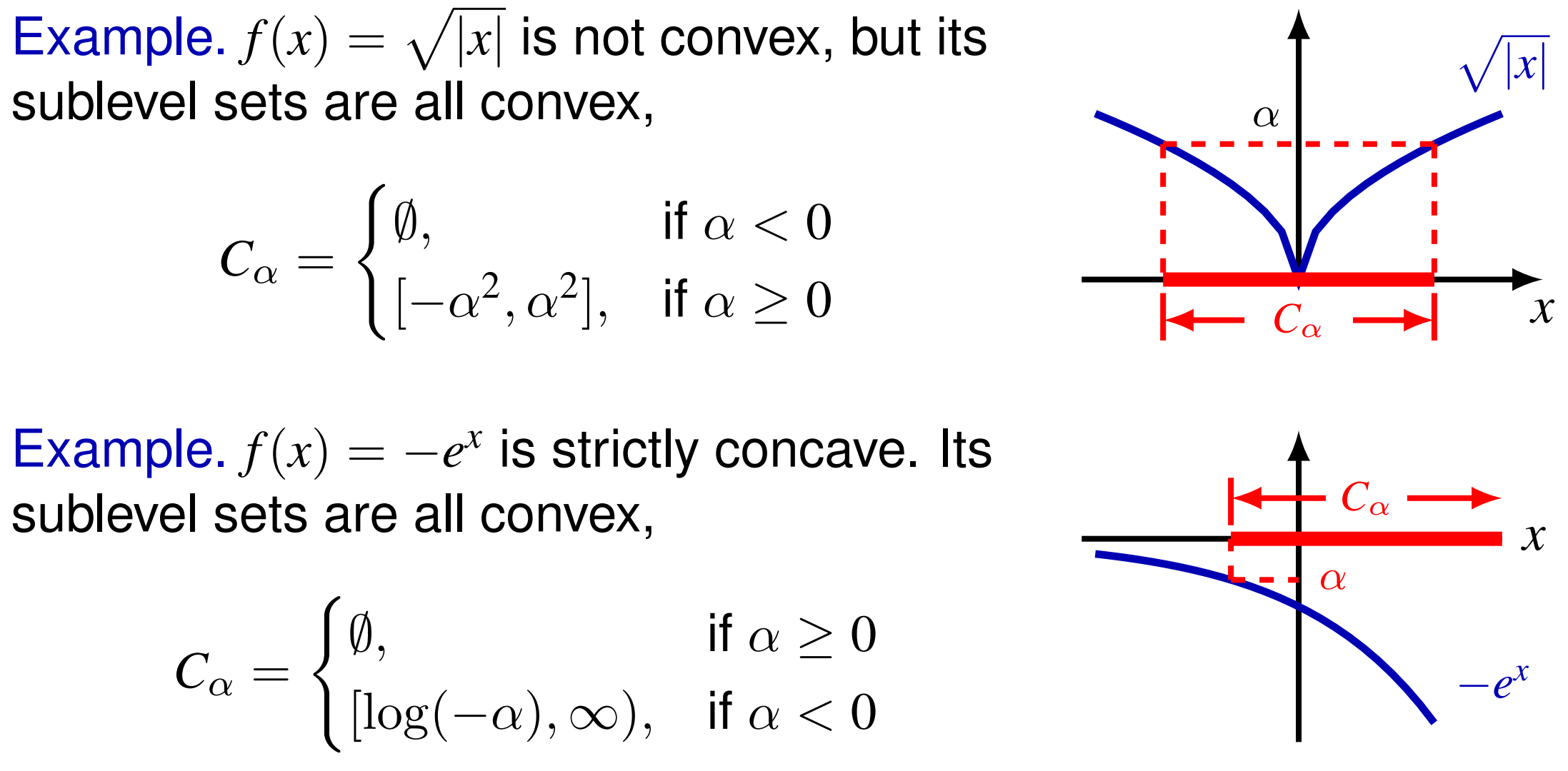
References