Berkshire Hathaway’s Performance vs. S&P 500 and NASDAQ 100
Berkshire Hathaway’s performance vs. S&P 500
The 17th page in 2023 Berkshire Hathaway annual report1 shows a comparison between Berkshire Hathaway’s Performance and dividends included S&P 500 index from 1965 to 2023, in total 59 years. (See Appendix. BTW, it’s actually a tradition of Berkshire to compare with S&P 500 in annual reports2.) I want to visualize it using Python in this post. Here is it.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import host_subplot
%config InlineBackend.figure_format = 'svg'
years = np.array(range(1965, 2024))
num_years = np.size(years)
berkshire = np.array([49.5, -3.4, 13.3, 77.8, 19.4,
-4.6, 80.5, 8.1, -2.5, -48.7,
2.5, 129.3, 46.8, 14.5, 102.5,
32.8, 31.8, 38.4, 69.0, -2.7,
93.7, 14.2, 4.6, 59.3, 84.6,
-23.1, 35.6, 29.8, 38.9, 25.0,
57.4, 6.2, 34.9, 52.2, -19.9,
26.6, 6.5, -3.8, 15.8, 4.3,
0.8, 24.1, 28.7, -31.8, 2.7,
21.4, -4.7, 16.8, 32.7, 27.0,
-12.5, 23.4, 21.9, 2.8, 11.0,
2.4, 29.6, 4.0, 15.8])
sp500 = np.array([10.0, -11.7, 30.9, 11.0, -8.4,
3.9, 14.6, 18.9, -14.8, -26.4,
37.2, 23.6, -7.4, 6.4, 18.2,
32.3, -5.0, 21.4, 22.4, 6.1,
31.6, 18.6, 5.1, 16.6, 31.7,
-3.1, 30.5, 7.6, 10.1, 1.3,
37.6, 23.0, 33.4, 28.6, 21.0,
-9.1, -11.9, -22.1, 28.7, 10.9,
4.9, 15.8, 5.5, -37.0, 26.5,
15.1, 2.1, 16.0, 32.4, 13.7,
1.4, 12.0, 21.8, -4.4, 31.5,
18.4, 28.7, -18.1, 26.3])
idx = np.array(range(0,num_years))
years, berkshire, sp500 = years[idx], berkshire[idx], sp500[idx]
berkshire_compound, sp500_compound = np.cumprod((berkshire/100)+1), np.cumprod((sp500/100)+1)
ax1 = host_subplot(111)
ax2 = ax1.twinx()
bar_width = 0.3
ax1.bar(years, berkshire, bar_width, alpha=0.7, label='Berkshire')
ax1.bar(years+bar_width, sp500, bar_width, alpha=0.7, label='SP500')
ax1.legend(loc='upper left', ncols=2)
xticks_x, xticks_y = years+bar_width/2, years
ax1.set_xticks(xticks_x[::7], xticks_y[::7])
ax1.set_xlabel('Years')
ax1.set_ylabel('Annual percentage change (%)')
ax2.plot(years, berkshire_compound)
ax2.plot(years, sp500_compound)
ax2.set_ylabel('Overall gain')
plt.title('Berkshire''s performance vs. S&P 500 ({}-{})'.format(years[0], years[-1]))
berkshire_ag = (berkshire_compound[-1] ** (1/np.size(idx)) - 1)*100
sp500_ag = (sp500_compound[-1] ** (1/np.size(idx)) - 1)*100
print("{}-{}".format(years[0], years[-1]))
print("{}: {:.2f} ".format("Total gain (Berkshire)", berkshire_compound[-1]))
print("{}: {:.2f}%".format("Compounded annual gain (Berkshire)", berkshire_ag))
print("{}: {:.2f}".format("Total gain (SP500)", sp500_compound[-1]))
print("{}: {:.2f}%".format("Compounded annual gain (SP500)", sp500_ag))
plt.savefig("fig.png", dpi=900, bbox_inches='tight')
plt.show()
1
2
3
4
5
1965-2023
Total gain (Berkshire): 43748.51
Compounded annual gain (Berkshire): 19.86%
Total gain (SP500): 308.53
Compounded annual gain (SP500): 10.20%

We can intuitively feel the staggering power of compound rate and how great Berkshire is under Buffett’s control.
Then, we have a detailed look at performance comparison in the past 20 years:
1
2
3
4
5
6
7
8
9
10
11
# ...
idx = np.array(range(num_years-20,num_years))
years, berkshire, sp500 = years[idx], berkshire[idx], sp500[idx]
# ...
xticks_x, xticks_y = years+bar_width/2, years
ax1.set_xticks(xticks_x, xticks_y, rotation=50)
# ...
1
2
3
4
5
2004-2023
Total gain (Berkshire): 6.43
Compounded annual gain (Berkshire): 9.75%
Total gain (SP500): 6.37
Compounded annual gain (SP500): 9.70%
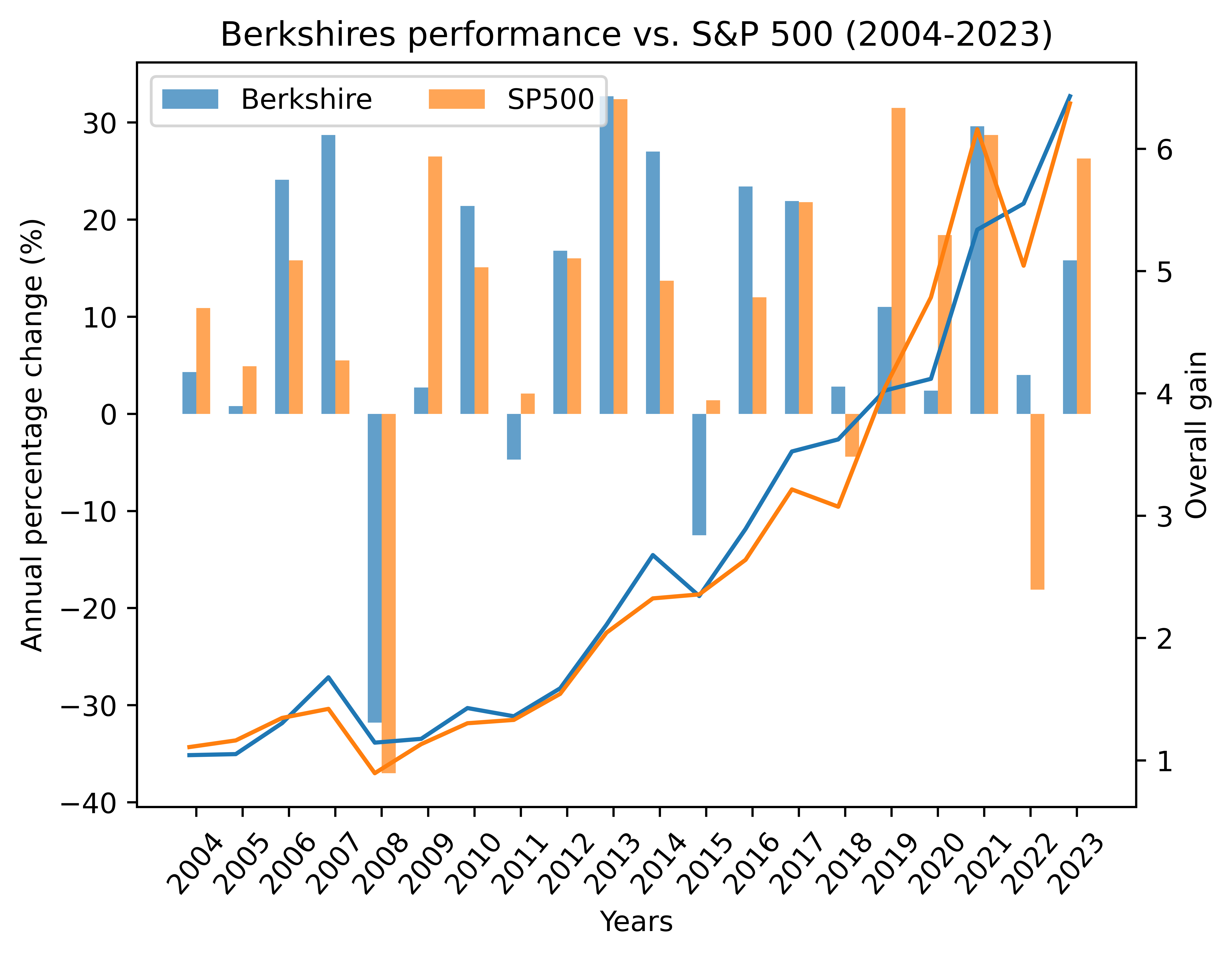
and that in the last 10 years:
1
2
3
4
5
2014-2023
Total gain (Berkshire): 3.05
Compounded annual gain (Berkshire): 11.79%
Total gain (SP500): 3.12
Compounded annual gain (SP500): 12.04%
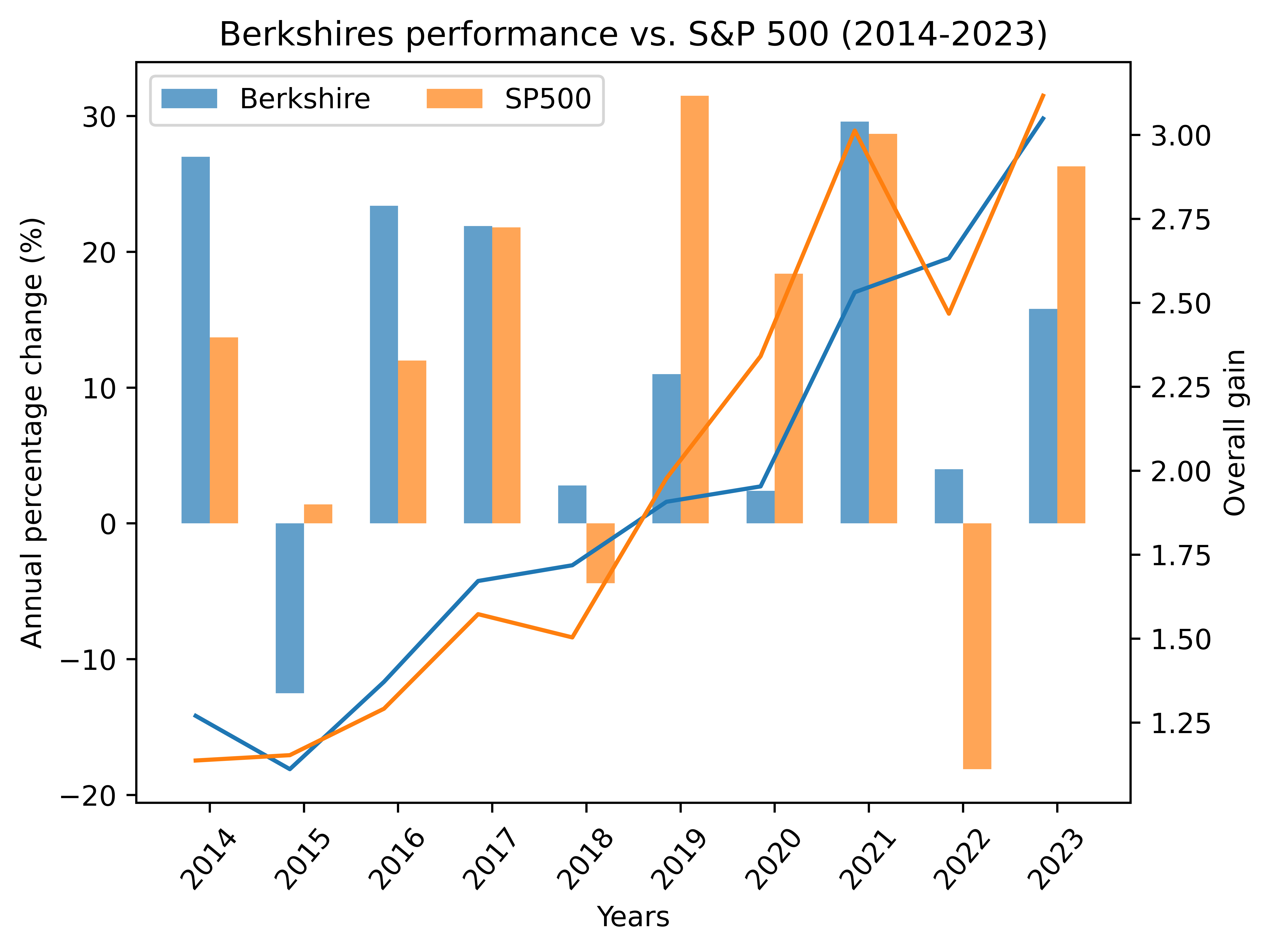
Berkshire Hathaway’s performance vs. NASDAQ 100
Yesterday (Dec. 9, 2024) , I found a website Slickcharts3, which is really close to my ideal website referenced for passive investing. It records “total returns by year” of S&P 500 (1926-2024)4, NASDAQ 100 (1986-2024)5, Dow Jones Industrial Average (1886-2024)6, and Berkshire (1981-2024)7.
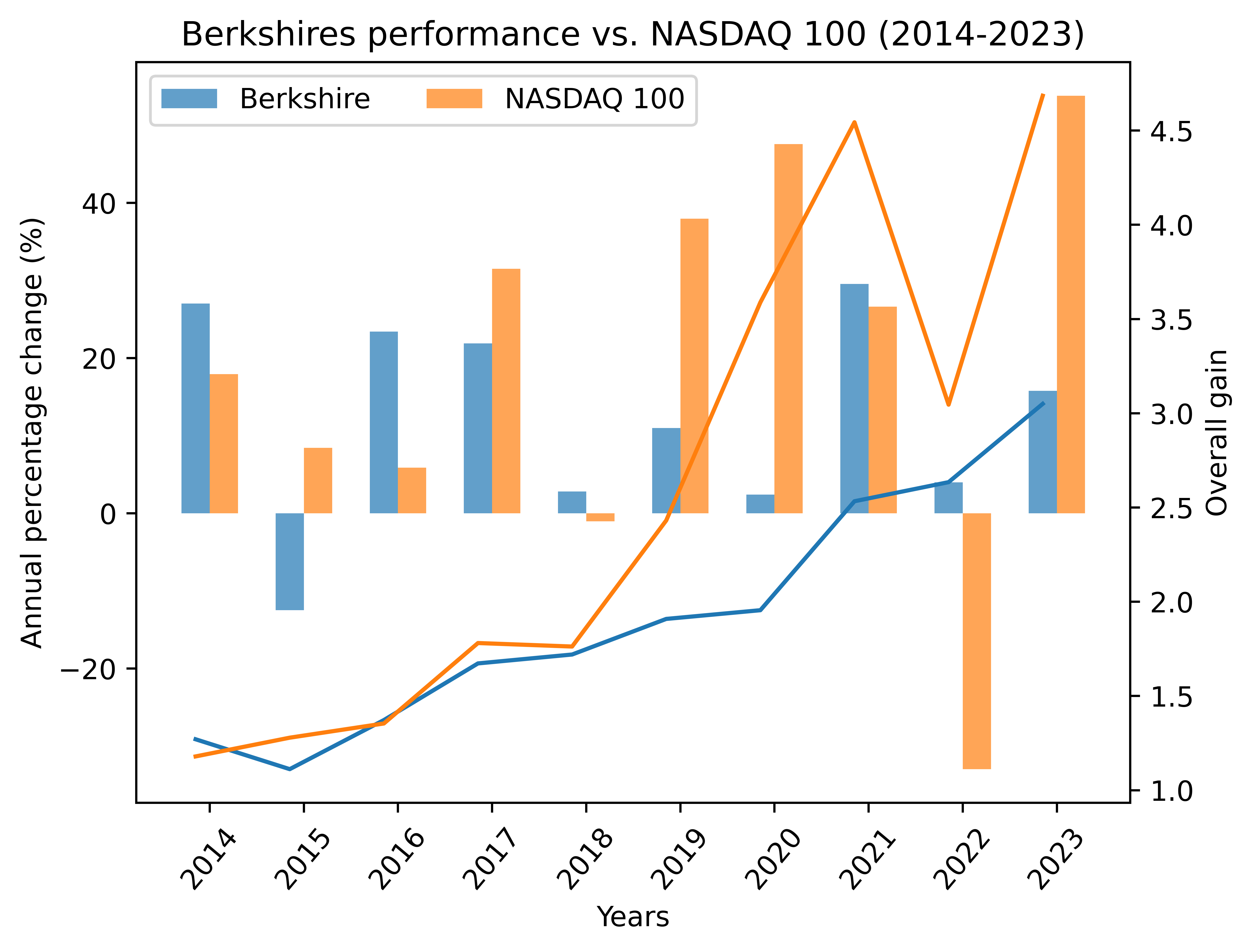
In the following text, I would compare Berkshire’s performance with NASDAQ 100 as I did as above. By the way, at this time the Berkshire’s annual returns I adopt are from website Slickcharts7, rather than official annual report.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import host_subplot
%config InlineBackend.figure_format = 'svg'
years = np.array(range(1986, 2024))
num_years = np.size(years)
berkshire = np.array([14.17, 4.61, 59.32, 84.57, -23.05,
35.58, 29.83, 38.94, 24.96, 57.35,
6.23, 34.90, 52.17, -19.86, 26.56,
6.48, -3.77, 15.81, 4.33, 0.82,
24.11, 28.74, -31.78, 2.69, 21.42,
-4.73, 16.82, 32.70, 27.04, -12.48,
23.42, 21.91, 2.82, 10.98, 2.42,
29.57, 4.00, 15.77])
nasaq100 = np.array([6.89, 10.50, 13.54, 26.17, -10.41,
64.99, 8.86, 10.58, 1.50, 42.54,
42.54, 20.63, 85.30, 101.95, -36.84,
-32.65, -37.58, 49.12, 10.44, 1.49,
6.79, 18.67, -41.89, 53.54, 19.22,
2.70, 16.82, 34.99, 17.94, 8.43,
5.89, 31.52, -1.04, 37.96, 47.58,
26.63, -32.97, 53.81])
idx = np.array(range(0,num_years))
years, berkshire, nasaq100 = years[idx], berkshire[idx], nasaq100[idx]
berkshire_compound, sp500_compound = np.cumprod((berkshire/100)+1), np.cumprod((nasaq100/100)+1)
ax1 = host_subplot(111)
ax2 = ax1.twinx()
bar_width = 0.3
ax1.bar(years, berkshire, bar_width, alpha=0.7, label='Berkshire')
ax1.bar(years+bar_width, nasaq100, bar_width, alpha=0.7, label='NASDAQ 100')
ax1.legend(loc='upper left', ncols=2)
xticks_x, xticks_y = years+bar_width/2, years
ax1.set_xticks(xticks_x[::7], xticks_y[::7])
ax1.set_xlabel('Years')
ax1.set_ylabel('Annual percentage change (%)')
ax2.plot(years, berkshire_compound)
ax2.plot(years, sp500_compound)
ax2.set_ylabel('Overall gain')
plt.title('Berkshire''s performance vs. NASDAQ 100 ({}-{})'.format(years[0], years[-1]))
berkshire_ag = (berkshire_compound[-1] ** (1/np.size(idx)) - 1)*100
sp500_ag = (sp500_compound[-1] ** (1/np.size(idx)) - 1)*100
print("{}-{}".format(years[0], years[-1]))
print("{}: {:.2f} ".format("Total gain (Berkshire)", berkshire_compound[-1]))
print("{}: {:.2f}%".format("Compounded annual gain (Berkshire)", berkshire_ag))
print("{}: {:.2f}".format("Total gain (NASDAQ 100)", sp500_compound[-1]))
print("{}: {:.2f}%".format("Compounded annual gain (NASDAQ 100)", sp500_ag))
plt.savefig("fig.png", dpi=900, bbox_inches='tight')
plt.show()
1
2
3
4
5
1986-2023
Total gain (Berkshire): 219.65
Compounded annual gain (Berkshire): 15.25%
Total gain (NASDAQ 100): 127.22
Compounded annual gain (NASDAQ 100): 13.60%
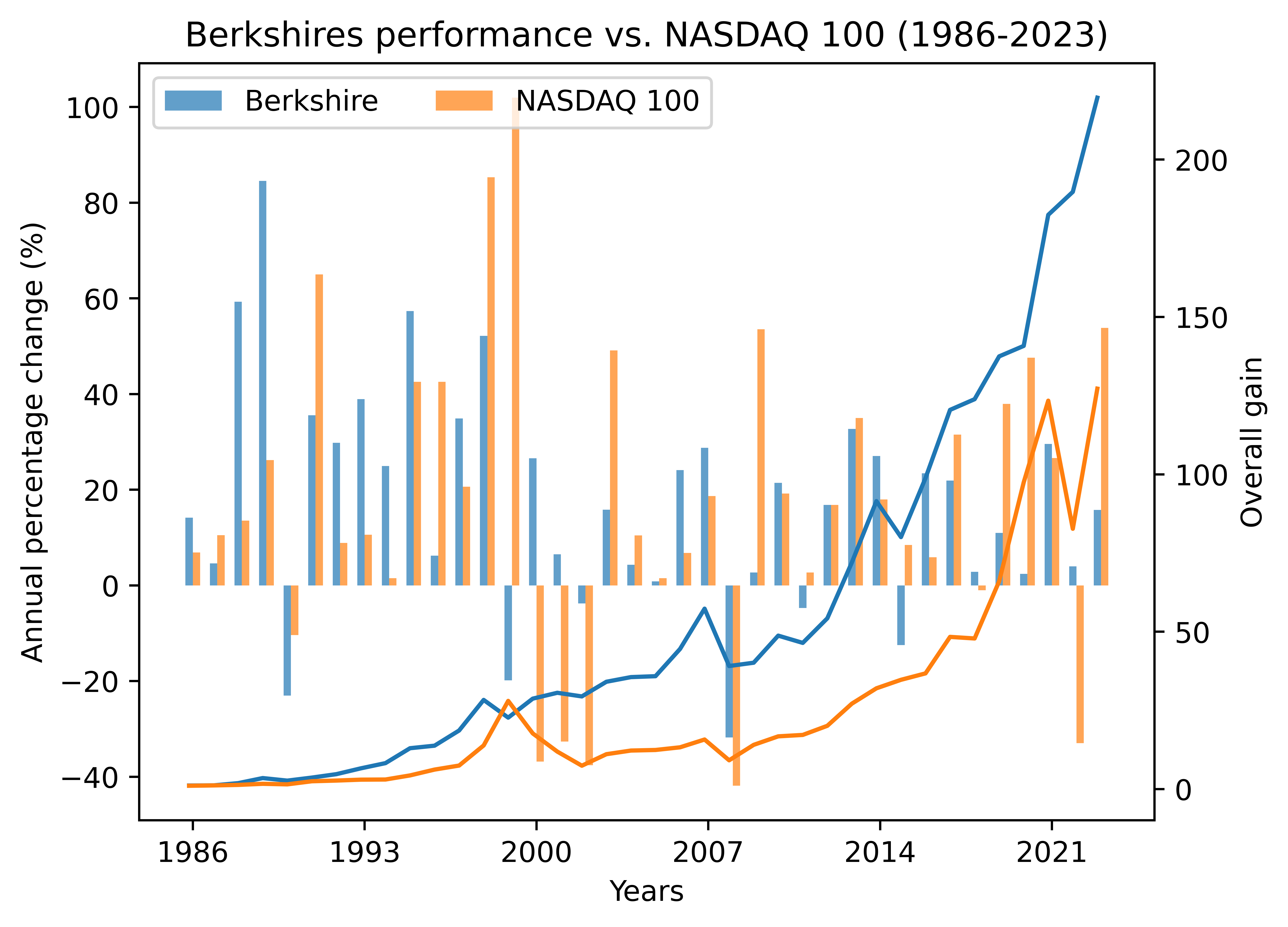
Similarly, we can have a comparison of the last 20 years:
1
2
3
4
5
6
7
8
9
10
11
# ...
idx = np.array(range(num_years-20,num_years))
years, berkshire, nasaq100 = years[idx], berkshire[idx], nasaq100[idx]
# ...
xticks_x, xticks_y = years+bar_width/2, years
ax1.set_xticks(xticks_x, xticks_y, rotation=50)
# ...
1
2
3
4
5
2004-2023
Total gain (Berkshire): 6.44
Compounded annual gain (Berkshire): 9.76%
Total gain (NASDAQ 100): 11.46
Compounded annual gain (NASDAQ 100): 12.97%
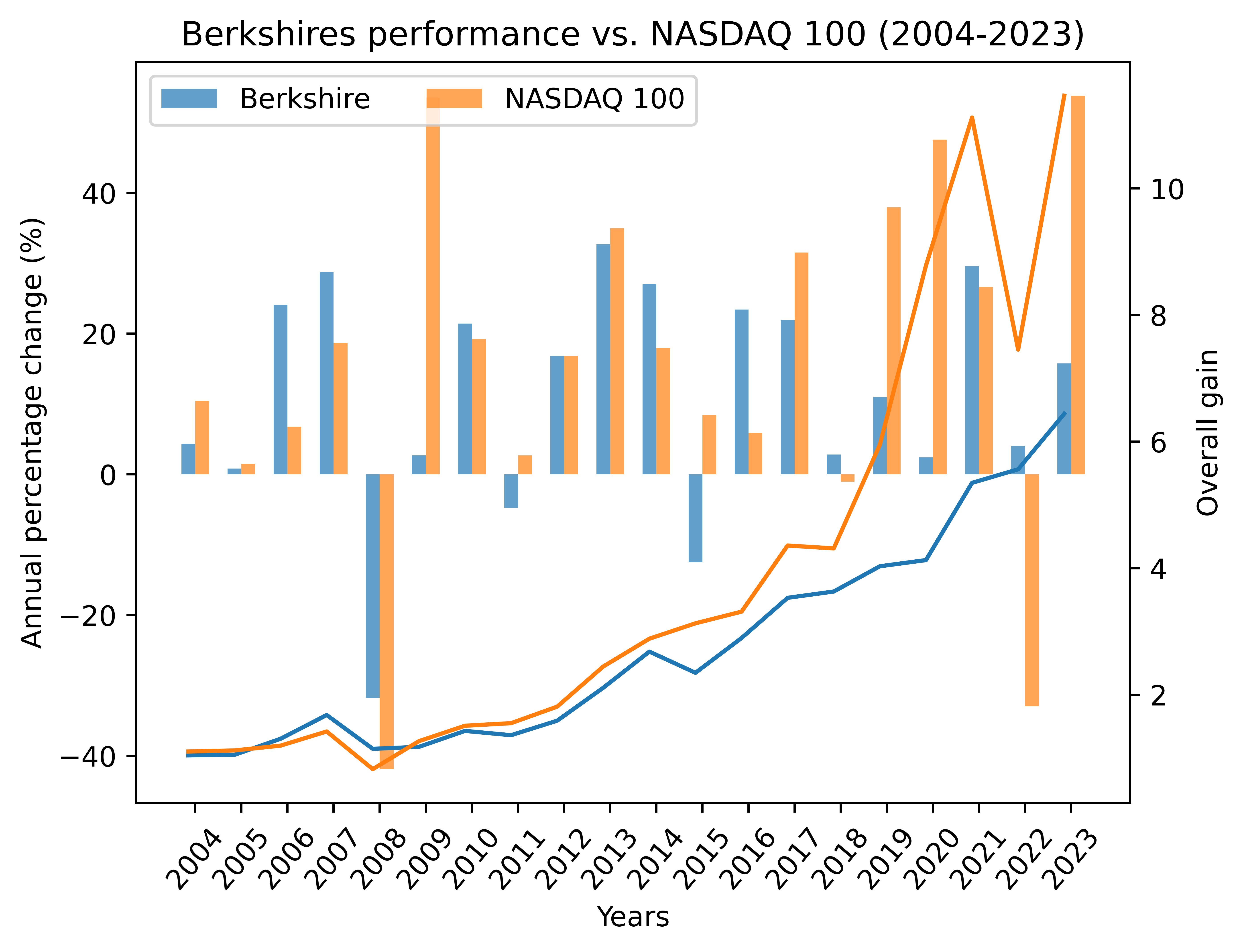
and the last 10 years:
1
2
3
4
5
2014-2023
Total gain (Berkshire): 3.05
Compounded annual gain (Berkshire): 11.80%
Total gain (NASDAQ 100): 4.68
Compounded annual gain (NASDAQ 100): 16.70%
The power of each compound interest
At last, take compounded annual gain of Berkshire and S&P 500 (19.86% and 10.20% respectively) and NASDAQ 100 (13.60%), we can calculate how \$1 compounds every 5 years with each compound interest.
1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
from pandas import DataFrame
years = np.array(range(5,65,5))
berkshire, sp500, nasdaq100 = (1+0.1986) ** years, (1+0.1020) ** years, (1+0.1360) ** years
data = DataFrame({'Years': years,
'Berkshire': berkshire,
'S&P 500': sp500,
'NASDAQ 100': nasdaq100})
data = data.set_index('Years')
print(data)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Berkshire S&P 500 NASDAQ 100
Years
5 2.473839 1.625204 1.891872
10 6.119878 2.641289 3.579178
15 15.139590 4.292635 6.771345
20 37.452901 6.976408 12.810516
25 92.652434 11.338089 24.235852
30 229.207171 18.426711 45.851119
35 567.021554 29.947171 86.744430
40 1402.719823 48.670273 164.109323
45 3470.102484 79.099138 310.473768
50 8584.473573 128.552263 587.376502
55 21236.602338 208.923695 1111.240921
60 52535.927219 339.543695 2102.325134
Note: In the annual report, the time period adopted when calculating “Compound Annual Gain” and “Overall Gain” is sort of different, reflected in that the former starts from 1965 while the latter 1964. This point should be noted when comparing them with my calculation results.
References