In blog¹ I ever learned the MATLAB official example “Physical System Modeling Using LSTM Network in Simulink”². In this example, the technician who wrote it says, “When you train an LSTM with very long sequences, the accumulation of the gradients computed for each time step can lead to vanishing gradients and cause the training process to converge to a suboptimal result. To prevent the gradients from vanishing, downsample the training data so that the sequences are much shorter without losing too much of the information.”

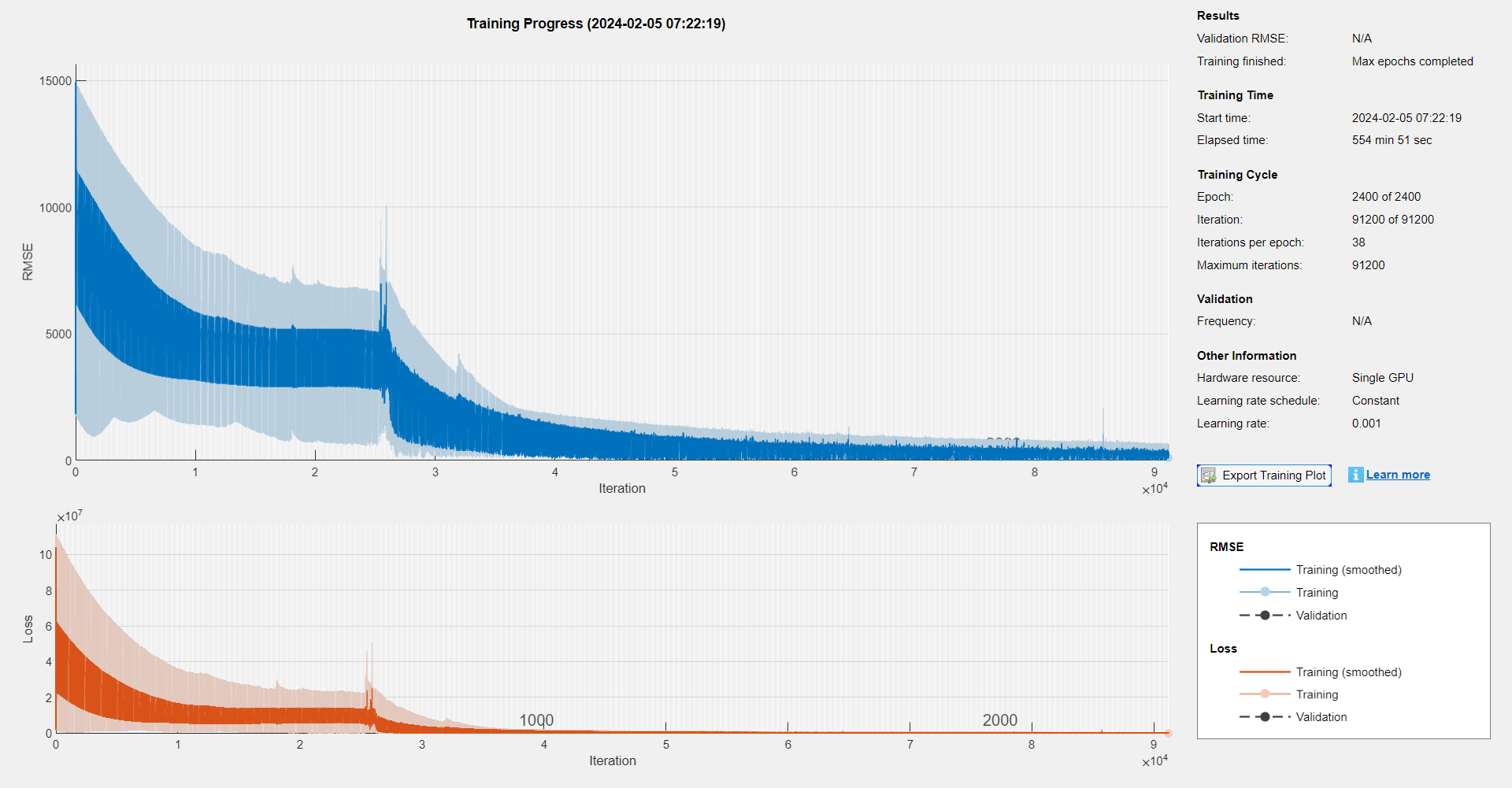
At that time, I just recorded it down, but not really understood this point deeply. Recently, I want to use an LSTM to fit the relationship between the input signals and the numeric labels, which is a regression task. The original signals, which has been preprocessed, are 5 ms and each of them has 10,000 sample points. To decrease the training time and save the memory, I downsampled the signals from 10,000 sample points to 2,000 points, and the training progress was like:

The structure of LSTM is very simple:

1
2
3
4
5
6
7
layers = [ ...
    sequenceInputLayer(1)

    bilstmLayer(numHiddenUnits,OutputMode="last")
    
    fullyConnectedLayer(width(labels))
    regressionLayer];

And it takes 554 min 51 sec to to reach the maximum training epochs.

Today I read the blog¹ again, and find the aforementioned words. I realize that although I made a downsample when processing the signals, but I didn’t note the problem of gradients vanishing: my purpose was just speeding up computation and saving the RAM.

In fact, 2,000-points signal is also too long. Imitating the example², I downsample the signal size to 200, and train another LSTM. The training progress is:

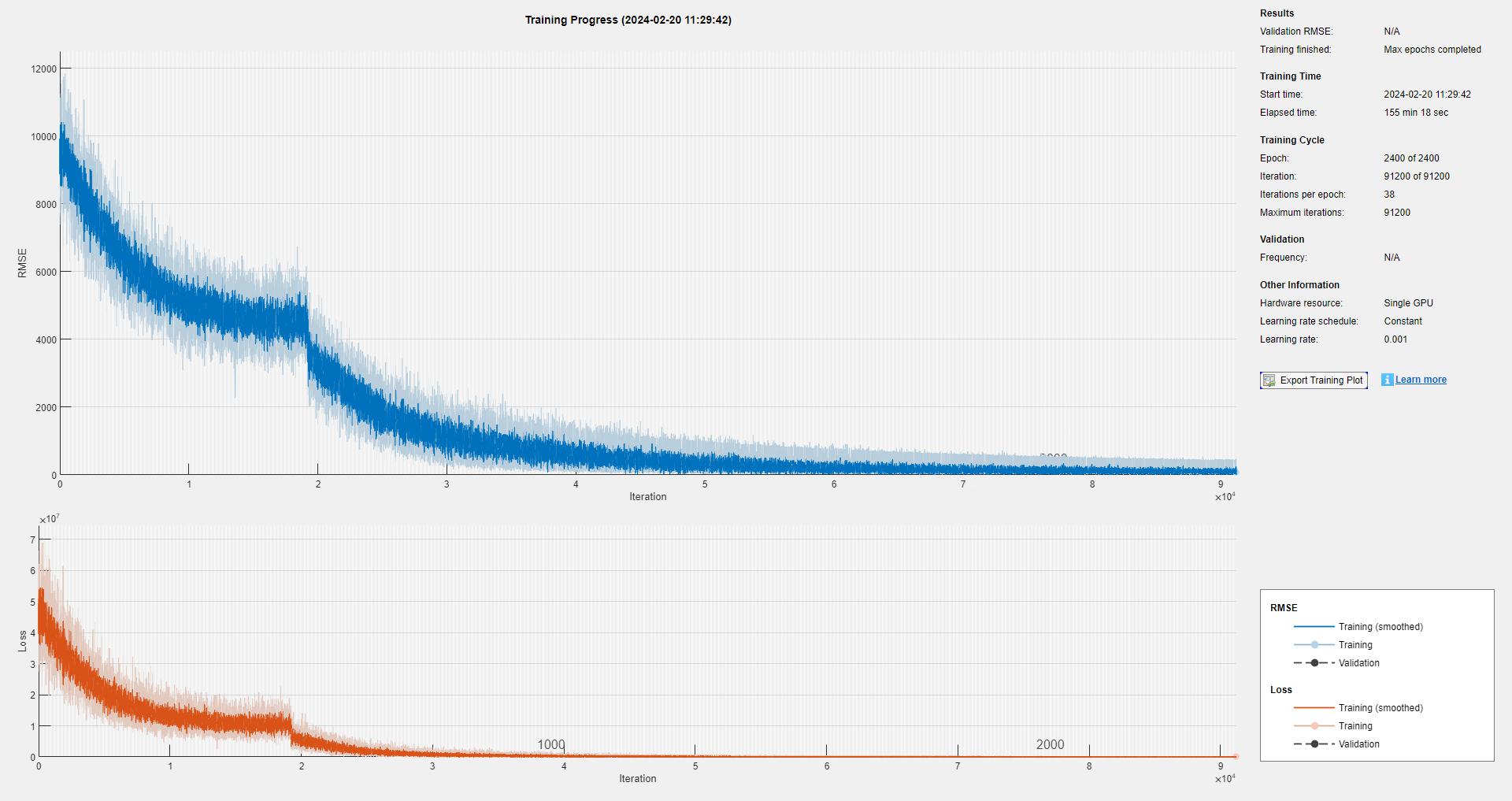
It only spend 155 min 18 sec, and the mini-batch RMSE and mini-batch loss decrease more rapidly, meaning that the problem of gradients vanishing has been relieved in a way.

By the way, for the MATLAB example² and the case that I meet, downsampling with a big interval don’t lead to losing much signal information; I suppose that this is because these signal don’t have many high frequency components. Maybe it’s not appropriate for other cases.

References