Elementary Matrix, Elementary Operation, and Gaussian Elimination
An elementary matrix corresponds to an elementary operation1:
An elementary matrix is a square matrix obtained from the application of a single elementary row operation to the identity matrix. … Left multiplication (pre-multiplication) by an elementary matrix represents elementary row operations, while right multiplication (post-multiplication) represents elementary column operations.
Take elementary row operations as examples, there are three kinds of operations, i.e.
- row switching
- row multiplication
- row addition
The definition, corresponding elementary matrix, and properties of each operation can be found in reference1. The following example compares the difference between the left multiplications (to show a series of elementary row operations) and the right multiplications (to show elementary column operations):
Left multiplications: elementary row operations
\[\begin{split} \begin{bmatrix} 1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\\ \end{bmatrix} &\rightarrow \begin{bmatrix} 0 & 1 & 0\\1 & 0 & 0\\0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\0 & -2 & 0\\0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 1 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\\ \end{bmatrix}\\ (R_3+R_2\rightarrow R_3)&\rightarrow \begin{bmatrix} 0 & 1 & 0\\1 & 0 & 0\\0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\0 & -2 & 0\\0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\\ 11 & 13 & 15 \end{bmatrix}\\ (-2R_2\rightarrow R_2)&\rightarrow \begin{bmatrix} 0 & 1 & 0\\1 & 0 & 0\\0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 2 & 3\\-8 & -10 & -12\\11 & 13 & 15\\ \end{bmatrix}\\ (R_2\leftrightarrow R_1)&\rightarrow \begin{bmatrix} -8 & -10 & -12\\ 1 & 2 & 3\\ 11 & 13 & 15\\ \end{bmatrix} \end{split}\notag\]Right multiplications: elementary column operations
\[\begin{split} \begin{bmatrix} 1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\\ \end{bmatrix} &\rightarrow \begin{bmatrix} 1 & 2 & 3\\4 & 5 & 6\\7 & 8 & 9\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 1 & 1\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\0 & -2 & 0\\0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 0 & 1 & 0\\1 & 0 & 0\\0 & 0 & 1\\ \end{bmatrix}\\ (C_3+C_2\rightarrow C_2)&\rightarrow \begin{bmatrix} 1 & 5 & 3\\4 & 11 & 6\\7 & 17 & 9\\ \end{bmatrix} \begin{bmatrix} 1 & 0 & 0\\0 & -2 & 0\\0 & 0 & 1\\ \end{bmatrix} \begin{bmatrix} 0 & 1 & 0\\1 & 0 & 0\\0 & 0 & 1\\ \end{bmatrix}\\ (-2C_2\rightarrow C_2)&\rightarrow \begin{bmatrix} 1 & -10 & 3\\ 4 & -22 & 6\\ 7 & -34 & 9\\ \end{bmatrix} \begin{bmatrix} 0 & 1 & 0\\1 & 0 & 0\\0 & 0 & 1\\ \end{bmatrix}\\ (C_2\leftrightarrow C_1)&\rightarrow \begin{bmatrix} -10 & 1 & 3\\-22 & 4 & 6\\-34 & 7 & 9\\ \end{bmatrix}\\ \end{split}\notag\]Besides, there is an important theorem about elementary matrix,
A square matrix $\boldsymbol{\mathrm{A}}$ is invertible if and only if it can be written as the product of elementary matrices.2
We can intuitively consider this matter–every invertible square matrix can be viewed as a result of a series of elementary operations on an identity matrix.
A practical case of applying elementary operations is using Gaussian elimination3 to solve linear equations. The Wikipedia article provides3 a very detailed example:
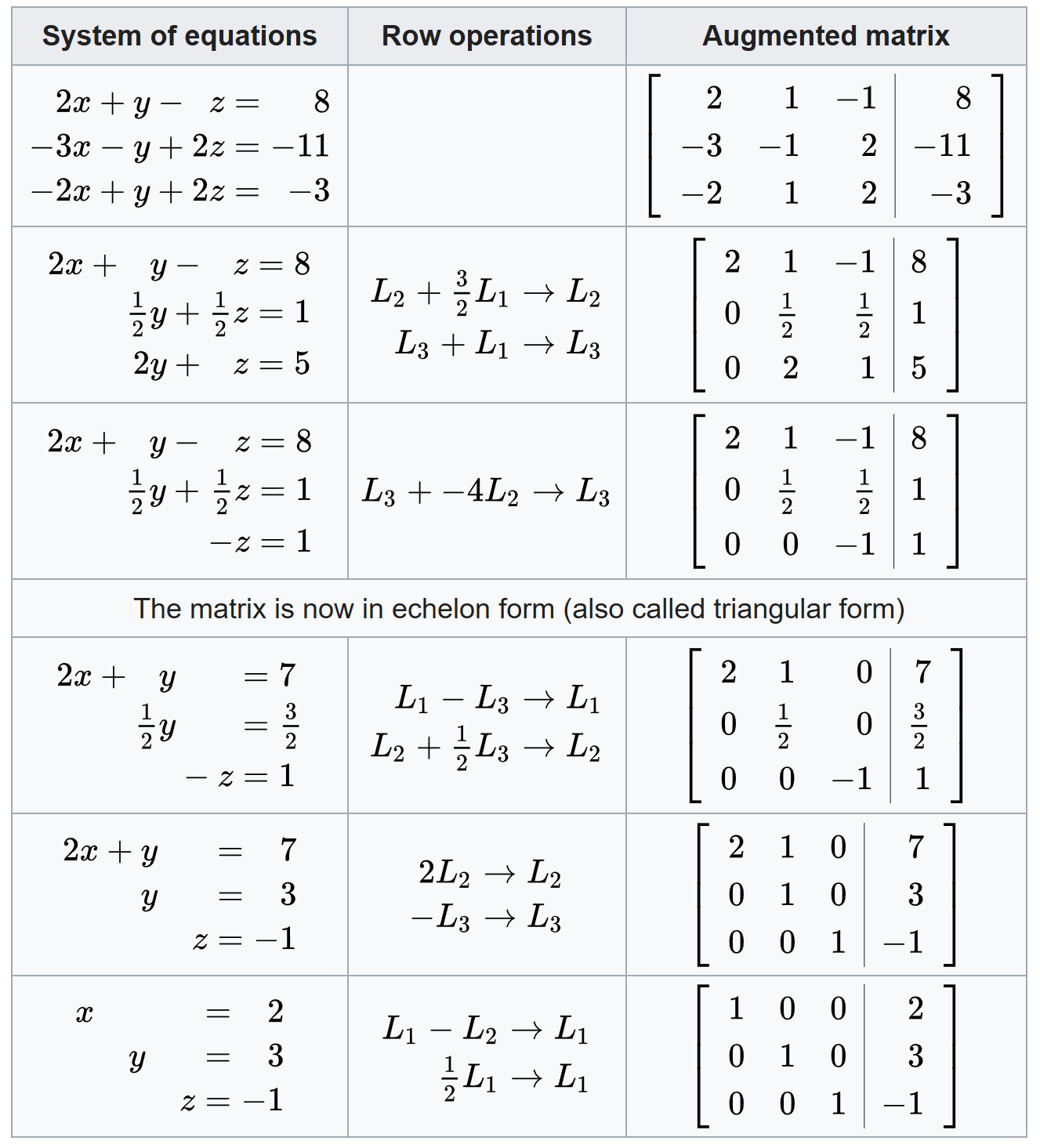
in which, the form like the matrix:
\[\begin{bmatrix} 2 & 1 & -1\\ 0 & \dfrac12 & \dfrac12\\ 0 & 0 & -1\\ \end{bmatrix}\notag\]is called the row echelon form4 (or triangular form), and the elimination to get this form is called Gaussian elimination. And the form of the final resulting matrix like:
\[\begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix}\notag\]is called the reduced row echelon form5, and this variant of Gaussian elimination that transforms a matrix to reduced row echelon form is sometimes called as Gauss–Jordan elimination4.
By the way, when explaining this example in the article3, a term “back-substitution” is used. It refers to the process that when the linear equation has been transformed into row echelon form or reduced row echelon form, the last equation should be solved first and then the next-to-last, etc.6
References