LaTeX Commands \overbrace and \underbrace
1
2
3
4
5
6
7
\documentclass{article}
\begin{document}
$\overbrace{a+b+c} = \underbrace{1+2+3}$
\end{document}
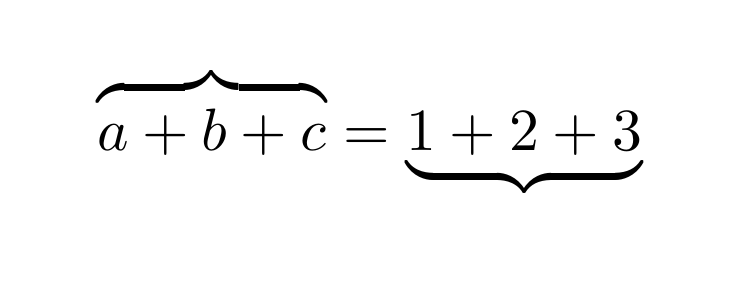
1
2
3
4
5
6
7
8
\documentclass{article}
\usepackage{amsmath}
\begin{document}
$ (\overbrace{a_0,a_1,\dots,a_n}^{\text{$n+1$ terms}}) = (\underbrace{0,0,\dots,0}_{n}, 1) $
\end{document}
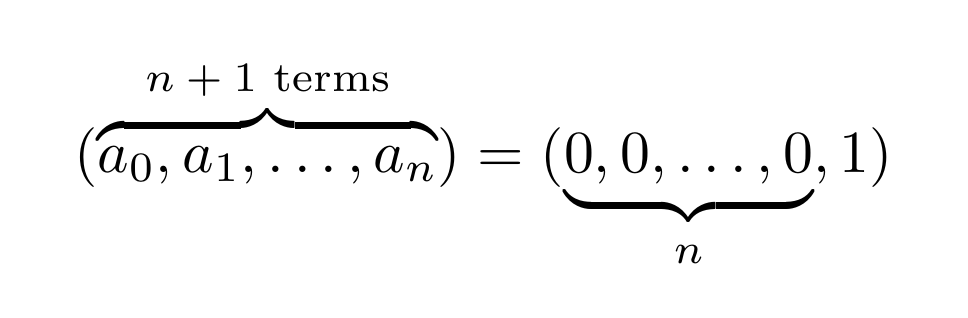
1
2
3
4
5
6
7
8
\documentclass{article}
\usepackage{amsmath, mathtools}
\begin{document}
$ \underbracket{\overbracket{1+2}^2+3}_3 $
\end{document}

1
2
3
4
5
6
7
8
9
10
\documentclass{article}
\usepackage{xcolor}
\begin{document}
\[ \color{red}{a+\lefteqn{\overbrace{\phantom{a+b+c}}^m}{b}} \]
\[ \color{blue}{+\underbrace{c+d+e}_n+f} \]
\[ \color{red}{a+\lefteqn{\overbrace{\phantom{a+b+c}}^m}{b}}+\color{blue}{\underbrace{c+d+e}_n+f} \]
\end{document}
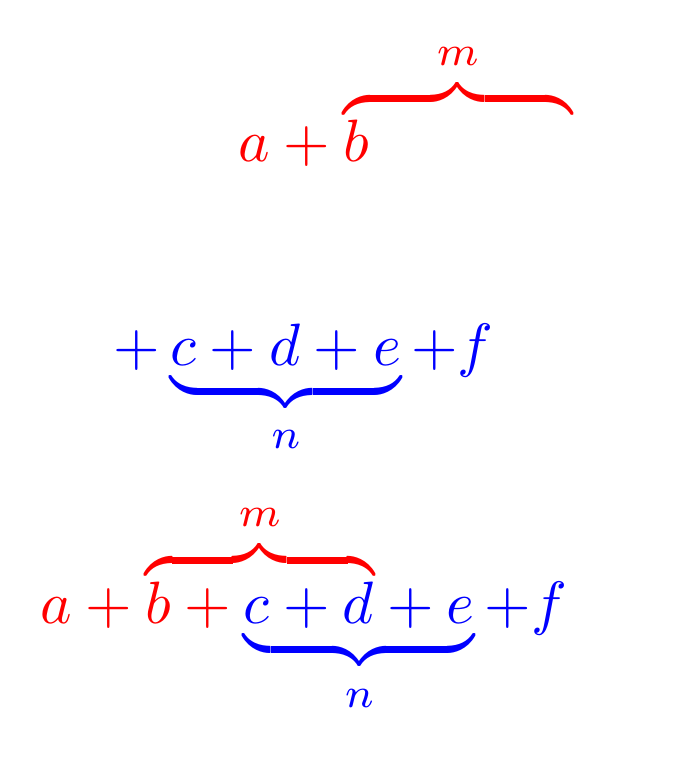
The command \lefteqn is used for splitting long formulas across lines. It typesets its argument in display style flush left in a box of zero width.1
\lefteqn{eqn} prints eqn in display math style, but pretends that it has zero width. It is typicaly used within an Eqnarray environment for displaying long equations that require multiple lines.2
\phantom{subformula}, \vphantom{subformula}, \hphantom{subformula}3
The \phantom command creates a box with the same height, depth, and width as subformula, but empty. That is, this command causes LaTeX to typeset the space but not fill it with the material. Here LaTeX will put a blank line that is the correct width for the answer, but will not show that answer.
The \vphantom variant produces an invisible box with the same vertical size as subformula, the same height and depth, but having zero width. And \hphantom makes a box with the same width as subformula but with zero height and depth.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
\documentclass{article}
\usepackage{xcolor}
\usepackage{amsmath, mathtools}
\begin{document}
\begin{align*}
y & = 2x^2 -3x +5\nonumber\\
& \hphantom{= \ 2\left(x^2-\frac{3}{2}\,x\right. }%
\textcolor{blue}{%
\overbrace{\hphantom{+\left(\frac{3}{4}\right)^2- %
\left(\frac{3}{4}\right)^2}}^{=0}}\nonumber\\[-11pt]
& = 2\left(\textcolor{red}{%
\underbrace{%
x^2-\frac{3}{2}\,x + \left(\frac{3}{4}\right)^2}%
}%
\underbrace{%
- \left(\frac{3}{4}\right)^2 + \frac{5}{2}}%
\right)\\
& = \left(\qquad\textcolor{red}{\left(x-\frac{3}{4}\right)^2}
\qquad + \ \frac{31}{16}\qquad\right)\nonumber\\
y\textcolor{blue}{-\frac{31}{8}}
& = 2\left(x\textcolor{cyan}{-\frac{3}{4}}\right)^2\nonumber
\end{align*}
\end{document}
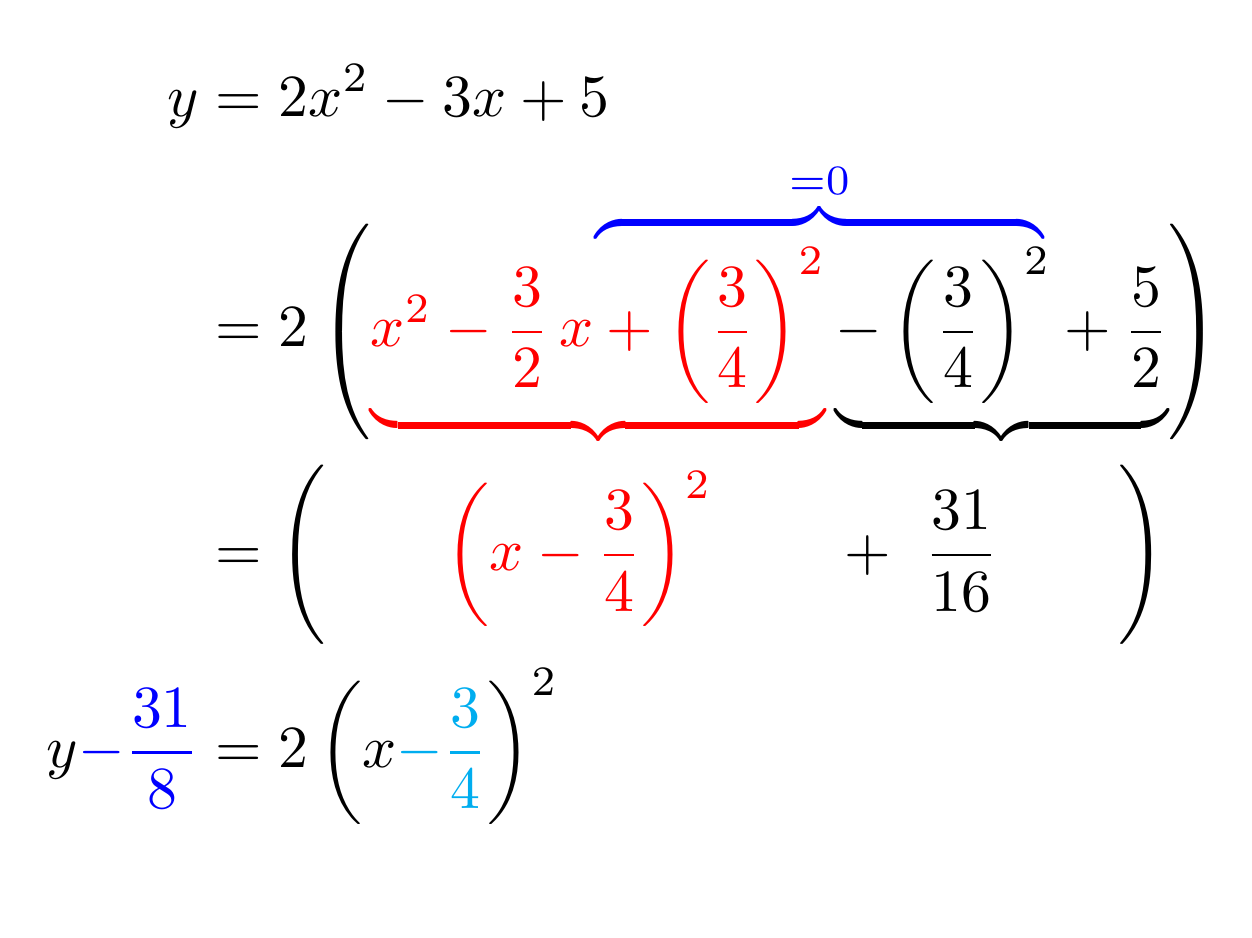
References