The Notion of First Principles in Philosophy, Mathematics, Physics, and Sciences
In philosophy and mathematics
As concluded in the Wikipedia entry “first principle”1:
In philosophy and science, a first principle is a basic proposition or assumption that cannot be deduced from any other proposition or assumption. First principles in philosophy are from first cause2 attitudes and taught by Aristotelians3, and nuanced versions of first principles are referred to as postulates by Kantians.
In mathematics and formal logic, first principles are referred to as axioms or postulates4.
…
In a formal logical system, that is, a set of propositions that are consistent with one another, it is possible that some of the statements can be deduced from other statements. For example, in the syllogism5, “All men are mortal; Socrates is a man; Socrates is mortal” the last claim can be deduced from the first two.
A first principle is an axiom that cannot be deduced from any other within that system. The classic example is that of Euclid’s Elements6; its hundreds of geometric propositions can be deduced from a set of definitions, postulates, and common notions: all three types constitute first principles.
…
In philosophy, “first principles” are from first cause attitudes commonly referred to as a priori terms and arguments, which are contrasted to a posteriori terms, reasoning, or arguments, in that the former are simply assumed and exist prior to the reasoning process, and the latter are deduced or inferred after the initial reasoning process. First principles are generally treated in the realm of philosophy known as epistemology7 but are an important factor in any metaphysical8 speculation.
In philosophy, “first principles” are often somewhat synonymous with a priori, datum, and axiomatic reasoning9.
…
Modern philosophy
Profoundly influenced by Euclid, Descartes10 was a rationalist who invented the foundationalist system of philosophy. He used the method of doubt, now called Cartesian doubt, to systematically doubt everything he could possibly doubt until he was left with what he saw as purely indubitable truths. Using these self-evident propositions as his axioms, or foundations, he went on to deduce his entire body of knowledge from them. The foundations are also called a priori truths. His most famous proposition is “Je pense, donc je suis” (“I think, therefore I am”, or “Cogito ergo sum”11), which he indicated in his Discourse on the Method was “the first principle of the philosophy of which I was in search.”
Descartes describes the concept of a first principle in the following excerpt from the preface to the Principles of Philosophy (1644):
I should have desired, in the first place, to explain in it what philosophy is, by commencing with the most common matters, as, for example, that the word philosophy signifies the study of wisdom, and that by wisdom is to be understood not merely prudence in the management of affairs, but a perfect knowledge of all that man can know, as well for the conduct of his life as for the preservation of his health and the discovery of all the arts, and that knowledge to subserve these ends must necessarily be deduced from first causes; so that in order to study the acquisition of it (which is properly called philosophizing), we must commence with the investigation of those first causes which are called Principles. Now, these principles must possess two conditions: in the first place, they must be so clear and evident that the human mind, when it attentively considers them, cannot doubt their truth; in the second place, the knowledge of other things must be so dependent on them as that though the principles themselves may indeed be known apart from what depends on them, the latter cannot nevertheless be known apart from the former. It will accordingly be necessary thereafter to endeavor so to deduce from those principles the knowledge of the things that depend on them, as that there may be nothing in the whole series of deductions which is not perfectly manifest.
from the perspective of philosophy and mathematics, the term “first principles” refers to as “axioms” or “postulates”, which are taken as true and hence starting point of a certain derivation. First principles, axioms, postulates; they are one and the same, but the term “first principles” seems not that commonly used compared to the other two, especially in mathematics.
When it comes to axioms, there are three classic examples that come to my mind.
(1) Probability axioms
The first is probability axioms. There are three the most fundamental probability axioms, which are the foundations of the whole probability theory introduced by Andrey Kolmogorov in 1933 (so they are also known as Kolmogorov axioms)12; starting from these three axioms, we can deduce every probability theorem and and lemma.
(2) Euclidean geometry vs. non-Euclidean geometry
The second is an understanding that, axioms can’t be proven to be correct, but by assuming different statements to be right and then adopting them as axioms, we could build up different mathematics. For example, Euclidean geometry takes five axioms13:
Let the following be postulated:
- To draw a straight line from any point to any point.
- To produce (extend) a finite straight line continuously in a straight line.
- To describe a circle with any centre and distance (radius).
- That all right angles are equal to one another.
- [The parallel postulate]: That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which the angles are less than two right angles.
where the fifth axiom is also called as the parallel postulate; many mathematician believe that it is too complicated to be an axiom. So, they propose replacing the parallel postulate with another axiom, which is not unique, or relaxing this requirement, then we’ll have non-Euclidean geometry14:
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.
So, for Euclidean geometry and non-Euclidean geometry, first principles are not the same.
(3) Hilbert’s program and Gödel’s incompleteness theorem
The third is Hilbert’s program15 and Gödel’s incompleteness theorems16. Hilbert’s program was intent to find a finite, complete set of axioms so that based on which all true mathematical statements can be deduced by logic. But Gödel’s incompleteness theorems give a negative answer.
in the early 1920s … Hilbert17 proposed to ground all existing theories to a finite, complete set of axioms, and provide a proof that these axioms were consistent. Hilbert proposed that the consistency of more complicated systems, such as real analysis, could be proven in terms of simpler systems. Ultimately, the consistency of all of mathematics could be reduced to basic arithmetic.15
Gödel’s incompleteness theorems, published in 1931, showed that Hilbert’s program was unattainable for key areas of mathematics. In his first theorem, Gödel showed that any consistent system with a computable set of axioms which is capable of expressing arithmetic can never be complete: it is possible to construct a statement that can be shown to be true, but that cannot be derived from the formal rules of the system. In his second theorem, he showed that such a system could not prove its own consistency, so it certainly cannot be used to prove the consistency of anything stronger with certainty. This refuted Hilbert’s assumption that a finitistic system could be used to prove the consistency of itself, and therefore could not prove everything else.
in detail15,
The main goal of Hilbert’s program was to provide secure foundations for all mathematics. In particular, this should include:
- A formulation of all mathematics; in other words all mathematical statements should be written in a precise formal language, and manipulated according to well defined rules.
- Completeness: a proof that all true mathematical statements can be proved in the formalism.
- Consistency: a proof that no contradiction can be obtained in the formalism of mathematics. This consistency proof should preferably use only “finitistic” reasoning about finite mathematical objects.
- Conservation: a proof that any result about “real objects” obtained using reasoning about “ideal objects” (such as uncountable sets) can be proved without using ideal objects.
- Decidability: there should be an algorithm for deciding the truth or falsity of any mathematical statement.
Kurt Gödel18 showed that most of the goals of Hilbert’s program were impossible to achieve, at least if interpreted in the most obvious way. Gödel’s second incompleteness theorem shows that any consistent theory powerful enough to encode addition and multiplication of integers cannot prove its own consistency. This presents a challenge to Hilbert’s program:
- It is not possible to formalize all mathematical true statements within a formal system, as any attempt at such a formalism will omit some true mathematical statements. There is no complete, consistent extension of even Peano arithmetic19 based on a computably enumerable set of axioms.
- A theory such as Peano arithmetic cannot even prove its own consistency, so a restricted “finitistic” subset of it certainly cannot prove the consistency of more powerful theories such as set theory.
- There is no algorithm to decide the truth (or provability) of statements in any consistent extension of Peano arithmetic. Strictly speaking, this negative solution to the Entscheidungsproblem appeared a few years after Gödel’s theorem, because at the time the notion of an algorithm had not been precisely defined.
Consistency, independence, and completeness are three properties of axiomatic system20:
An axiomatic system is said to be consistent if it lacks contradiction. That is, it is impossible to derive both a statement and its negation from the system’s axioms. Consistency is a key requirement for most axiomatic systems, as the presence of contradiction would allow any statement to be proven (principle of explosion).
In an axiomatic system, an axiom is called independent if it cannot be proven or disproven from other axioms in the system. A system is called independent if each of its underlying axioms is independent. Unlike consistency, independence is not a necessary requirement for a functioning axiomatic system — though it is usually sought after to minimize the number of axioms in the system.
An axiomatic system is called complete if for every statement, either itself or its negation is derivable from the system’s axioms (equivalently, every statement is capable of being proven true or false).
Peano arithmetic is actually very fundamental–the axiomatization of arithmetic provided by Peano axioms is commonly called Peano arithmetic. In which there are nine Peano axioms19:
The nine Peano axioms contain three types of statements.
The first axiom asserts the existence of at least one member of the set of natural numbers.
(1) $0$ is a natural number.
The next four are general statements about equality; in modern treatments these are often not taken as part of the Peano axioms, but rather as axioms of the “underlying logic”.
(2) For every natural number $x$, $x = x$. That is, equality is reflexive.
(3) For all natural numbers $x$ and $y$, if $x = y$, then $y = x$. That is, equality is symmetric.
(4) For all natural numbers $x$, $y$ and $z$, if $x = y$ and $y = z$, then $x = z$. That is, equality is transitive.
(5) For all $a$ and $b$, if $b$ is a natural number and $a = b$, then $a$ is also a natural number. That is, the natural numbers are closed under equality.
The remaining axioms define the arithmetical properties of the natural numbers. The naturals are assumed to be closed under a single-valued “successor” function $S$.
The next three axioms are first-order statements about natural numbers expressing the fundamental properties of the successor operation.
(6) For every natural number $n$, $S(n)$ is a natural number. That is, the natural numbers are closed under $S$.
(7) For all natural numbers $m$ and $n$, if $S(m) = S(n)$, then $m = n$. That is, $S$ is an injection.
(8) For every natural number $n$, $S(n) = 0$ is false. That is, there is no natural number whose successor is $0$.
The ninth, final, axiom is a second-order statement of the principle of mathematical induction over the natural numbers, which makes this formulation close to second-order arithmetic.
The intuitive notion that each natural number can be obtained by applying successor sufficiently many times to zero requires an additional axiom, which is sometimes called the axiom of induction.
(9) If $K$ is a set such that:
- $0$ is in $K$, and
- for every natural number $n$, $n$ being in $K$ implies that $S(n)$ is in $K$,
then $K$ contains every natural number.
The induction axiom is sometimes stated in the following form:
(9) If $\varphi$ is a unary predicate such that:
- $\varphi(0)$ is true, and
- for every natural number $n$, $\varphi(n)$ being true implies that $\varphi(S(n))$ is true,
then $\varphi(n)$ is true for every natural number $n$.
All in all, Gödel’s incompleteness theorems state that we can’t find a finite complete set of axioms for mathematics, and also prove that the axiomatization, as a means, is limited.
In physics and sciences
In physics and sciences, the term “first principles” refers to the work purely based on theories without relying on empirical model and parameter fitting.
In physics and other sciences, theoretical work is said to be from first principles, or ab initio21, if it starts directly at the level of established science and does not make assumptions such as empirical model and parameter fitting. For example, calculation of electronic structure using Schrödinger’s equation within a set of approximations that do not include fitting the model to experimental data is an ab initio approach.
As the opposite of first principles modeling, the methods of empirical model and parameter fitting are widely used in the fields of engineering, like Paschen’s law22 and lightning strike modeling in electrical engineering for example. In addition, the distinction between these two types of methods reminds me of four science paradigms proposed by computer scientist Jim Gray232425:
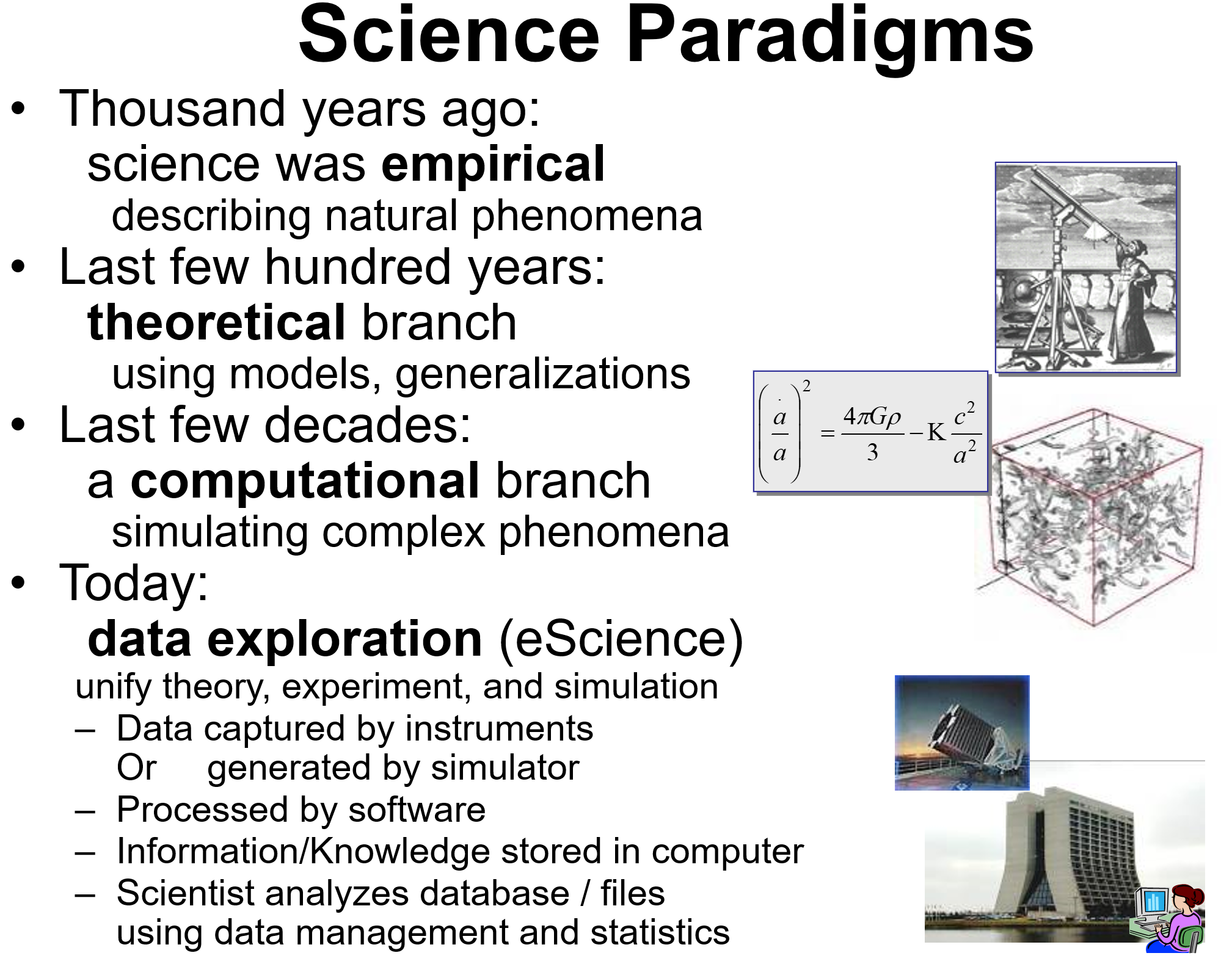
They follow different science paradigms. Or, maybe not that strict, first principles modeling is model-based, while empirical model along with parameter fitting are data-driven.
First principles thinking
Another term related to “first principles” is “first principles thinking”:
“First principles thinking” consists of decomposing things down to the fundamental axioms in the given arena, before reasoning up by asking which ones are relevant to the question at hand, then cross referencing conclusions based on chosen axioms and making sure conclusions do not violate any fundamental laws. Physicists include counterintuitive concepts with reiteration.1
Sometimes called “reasoning from first principles,” first principles thinking is the practice of questioning every assumption you think you know about a given problem, then creating new solutions from scratch. It’s one of the best ways to unlock creative solutions to complicated problems.
Take the NFL coach, for example. They combine the basic rules of football with the capabilities of their players to create entirely new plays for their team. Because the coach understands the first principles that built the play, they are able to identify why it was successful or unsuccessful—and adjust as necessary.26
which advocates to identify and challenge the fundamental assumptions of problem to be solved and based on which, propose targeted solutions.
References
-
Unmoved mover (First cause): The unmoved mover or prime mover is a concept advanced by Aristotle as a primary cause (or first uncaused cause) or “mover” of all the motion in the universe. As is implicit in the name, the unmoved mover moves other things, but is not itself moved by any prior action. ˄
-
Aristotelianism: Aristotelianism is a philosophical tradition inspired by the work of Aristotle, usually characterized by deductive logic and an analytic inductive method in the study of natural philosophy and metaphysics. ˄
-
Axiom: An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. ˄
-
Axiomatic system: In mathematics and logic, an axiomatic system is any set of primitive notions and axioms to logically derive theorems. A theory is a consistent, relatively-self-contained body of knowledge which usually contains an axiomatic system and all its derived theorems. An axiomatic system that is completely described is a special kind of formal system. A formal theory is an axiomatic system (usually formulated within model theory) that describes a set of sentences that is closed under logical implication. A formal proof is a complete rendition of a mathematical proof within a formal system. ˄
-
Cogito, ergo sum: … As Descartes explained in a margin note, “we cannot doubt of our existence while we doubt.” … Descartes’s statement became a fundamental element of Western philosophy, as it purported to provide a certain foundation for knowledge in the face of radical doubt. While other knowledge could be a figment of imagination, deception, or mistake, Descartes asserted that the very act of doubting one’s own existence served—at minimum—as proof of the reality of one’s own mind; there must be a thinking entity—in this case the self—for there to be a thought. ˄
-
What Is First Principles Thinking? 3 Popular Approaches and How to Apply Them. ˄