IntroductionPermalink

Recently, I’ve been reading Tsung-Yi Lin¹ et al.’s paper, Focal Loss for Dense Object Detection² (Best Student Paper Award in 2017 ICCV). In their ablation experiments for testing Focal Loss, several metrics were adopted to evaluate detectors, like $\text{AP}$, ${\text{AP}}_{50}$, ${\text{AP}}_{75}$, ${\text{AP}}_{\mathrm{S}}$, ${\text{AP}}_{\mathrm{M}}$, ${\text{AP}}_{\mathrm{L}}$:

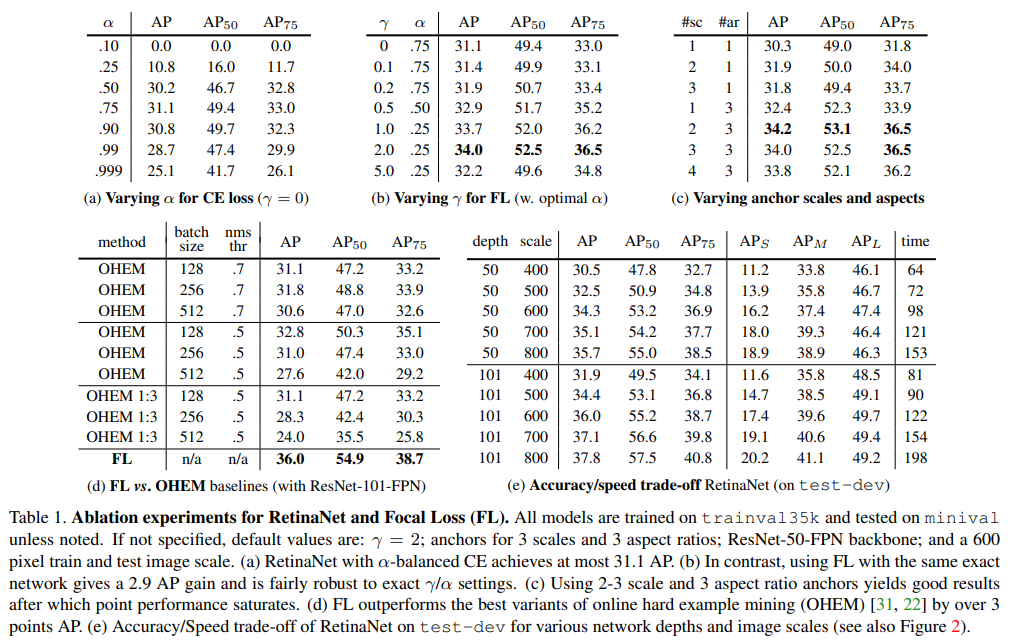
These metrics are so commonly used in object detection that they didn’t give any explicit explanation. But I am totally fresh in this area, and have no idea about them. This is why I write this post.

AP is the abbreviation for Average Precision, but it’s actually not the average of detection precision, which looks reasonable according to its literal meaning. Rather, like the notion of AUC for ROC curve (TPR-FPR) in classification task, AP is also computed based on a specific curve, that is precision-recall curve.

Due to that I ever learned ROC curve in classification problem in detail (see my previous blog³), so when I first knew about AP, I realized that it is a good start to introduce it from the concept of ROC curve. Therefore, in the following text, I would first explain ROC curve briefly. Then, AP and some metrics related to it will be introduced. Besides, AR, i.e., Average Recall, is also usually used for evaluating detectors, and it has the similar calculation method with AP. So, I would make some explanations about it as well.

The concepts of ROC curve and AUC in binary classification taskPermalink

In the binary classification task, a classifier after training can output predicted possibilities (more precisely, say scores) for the input observations. Researchers can set a threshold, and those observations whose corresponding scores are over/below the specified threshold can be labeled as positive/negative. Then, according to the true labels and corresponding predicted labels for observations, we can obtain a 2-by-2 confusion matrix, classifying each observation as TP (True positive), FN (False negative), FP (False positive), or TN (True negative), and hence TPR (True positive rate, or say recall) and FPR (False positive rate) can be calculated:

By varying the specified threshold, we can obtain different TPR-FPR pairs, and based on which an ROC (Receiver Operating Characteristic) curve, showing how TPR changes as FPR, can be plotted. The area under the ROC curve (also known as AUC), that is the integral of ROC curve over the interval $\text{FPR}\in [0,1]$, is a metric that can reflect the average performance of the classifier.

More detailed information concerning ROC and AUC can be found in my previous blog³.

AP and AP-related metricsPermalink

Average Precision (AP): AUC of precision-recall curvePermalink

In object detection tasks, the detector usually predicts bounding boxes and corresponding class labels⁴. AP and some related metrics are to evaluate the performance of detectors predicting bounding boxes.

Take single object detection.

The true position of bounding boxes (usually is annotated by hands) is called ground truth bounding box, and the predicted position is predicted bounding box ⁵⁶:

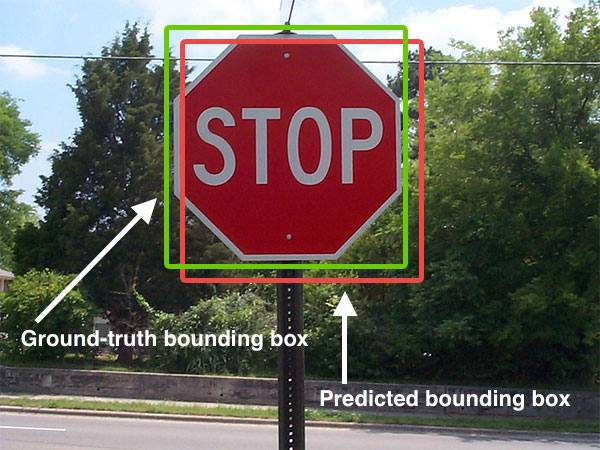
By Adrian Rosebrock, CC BY-SA 4.0, Link.

Based on them, we can define the notion of Intersection over Union (IoU) as follows⁷:

By Adrian Rosebrock, CC BY-SA 4.0, Link.

Apparently, different cases will yields different IoU values (range from [0,1]), for example⁸,

By Adrian Rosebrock, CC BY-SA 4.0, Link.

Here, if adopt different IoU thresholds, we can classify the predicted detection results as TP or FP.

Take the above case. If we set threshold as 0.5, then we have:

and if the threshold is 0.8, then:

In target detection, where kind of different from constructing the ROC curve based on TPR-FPR pairs in classification task, we hope to obtain a precision-recall curve (p-r curve, or $p(r)$​). Among which, the definition of precision is⁹:

and the definition of recall is the same as Eq. $\text{(1)}$, and FN in Eq. $\text{(1)}$ represents the case that “a detector does not detect an object that is present—either by silently failing to detect the object’s presence entirely, or by miscalculating the object’s location or classification”¹⁰, or rather, “If a ground-truth bounding box has no TP detection to math with, it is labeled as a false negative FN.”¹¹

For aforementioned two cases, assuming that FN is 2 in both cases, then precision-recall pairs are $(0.67,0.5)$ and $(0.33,0.33)$, respectively. By varying IoU thresholds more densely, more precision-recall pairs can be calculated, and hence $p(r)$ plotted.

Similar to the definition of AUC made for ROC curve in binary classification task, for object detection, “Average Precision (AP) computes the average value of $p(r)$ over the interval from $r=0$ to $r=1$​​, that is the area under the precision-recall curve”¹².

Note that, in practice, the starting point of the integration interval is usually selected as 0.5 rather than 0. This point will be explained later.

AP-related metrics: ${\text{AP}}^{\text{IoU}=.50}$, ${\text{AP}}^{\text{IoU}=.75}$, ${\text{AP}}^{\text{small}}$, ${\text{AP}}^{\text{medium}}$, and ${\text{AP}}^{\text{large}}$Permalink

COCO (Common Objects in Context) official website provides an webpage to give more detailed information about evaluation metrics¹³, in addition to AP, there are some others related to it:

It’s not hard to figure out that, the metrics ${\text{AP}}_{50}$, ${\text{AP}}_{75}$, ${\text{AP}}_{\mathrm{S}}$, ${\text{AP}}_{\mathrm{M}}$, and ${\text{AP}}_{\mathrm{L}}$ in Lin’s paper correspond to ${\text{AP}}^{\text{IoU}=.50}$, ${\text{AP}}^{\text{IoU}=.75}$, ${\text{AP}}^{\text{small}}$, ${\text{AP}}^{\text{medium}}$, and ${\text{AP}}^{\text{large}}$ in the above table, respectively.

After learning previous content, it’s OK for me to understand what do $\text{AP}$, ${\text{AP}}_{\mathrm{S}}$, ${\text{AP}}_{\mathrm{M}}$ and ${\text{AP}}_{\mathrm{L}}$ mean and how they work. For example, for those metrics belonging to “AP Across Scales” part, AP-related metrics are used to judge whether or not detectors behave well for detecting small ($\text{area}<{32}^2$), medium (${32}^2<\text{area}<{96}^2$), and large ($\text{area}>{96}^2$) objects.

However, I still feel confused about ${\text{AP}}^{\text{IoU}=.50}$ and ${\text{AP}}^{\text{IoU}=.75}$. I’ve found some other references, but they all point out that AP metrics are computed based on the precision-recall curve¹⁴¹⁵, but how to determine a precision-recall curve based on only one precision-recall pair which is calculated by setting IoU threshold as 0.5 or 0.75? So finally, I make a guess that, maybe in these cases, precision-recall curve is horizontal line. Or rather, the precision always keeps the same with the precision value calculated based on setting threshold as 0.5/0.75 although recall changes, so that the area under the precision-recall curve is simply rectangular.

AR and AR-related metricsPermalink

Average Recall (AR): AUC of recall-IoU curvePermalink

As can be seen from Table I, besides AP, COCO detection challenge also take AR-related metrics.

AR is the abbreviation for Average Regression. According to Zenggyu’s blog¹⁶, like how we create the precision-recall curve while calculating AP, we can obtain a series of recall values by varying IoU thresholds. A recall-IoU curve can be plotted based on recall-IoU pairs, and the AUC of this recall-IoU curve is so-called AR, which can be expressed as (in continuous form):

where $o$ is IoU threshold and $\text{recall}(o)$ is the corresponding recall.

Eq. $\text{(6)}$ is consistent with the paper, What makes for effective detection proposals?¹⁷, which is referred by COCO evaluation documentation¹³ when introducing AR metric (actually it is the paper proposing AR metrics):

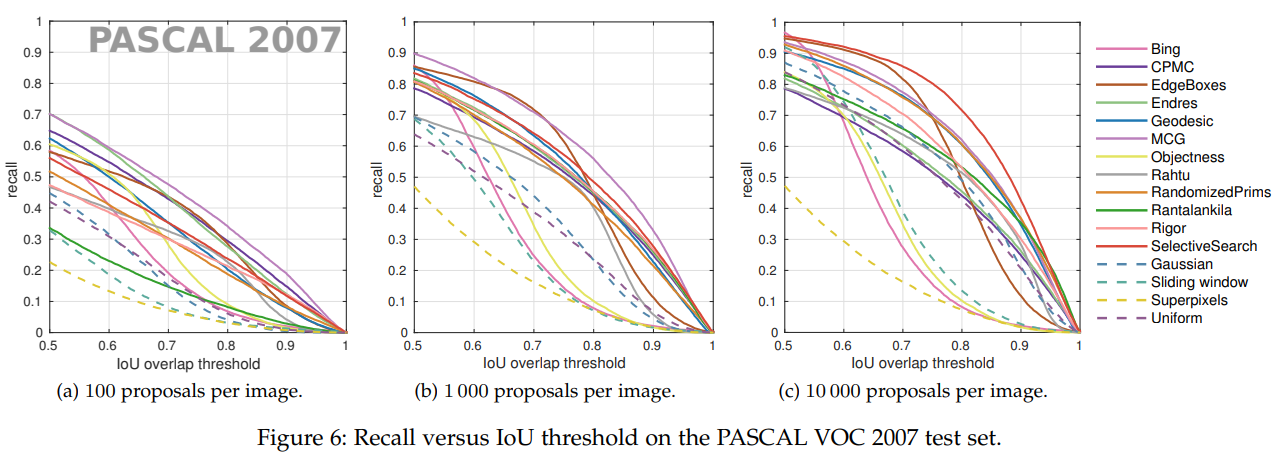
AR-related metrics: ${\text{AR}}^{\text{max}=1}$, ${\text{AR}}^{\text{max}=10}$, and ${\text{AR}}^{\text{max}=100}$Permalink

If understand AP, it’s not difficult to understand how AR is computed. However, as for the specific meaning of “${\text{AR}}^{\text{max}=\text{X}}$: AR given X (1/10/100) detection(s) per image” in Table I, I am not that sure.

Some references explain about them, like Picsellia’s blog¹⁸:

which says that “X” is the confidence threshold that used to determined whether a prediction is considered a true positive or false positive, and that will influence recall values. But it seems not much clear, at least for me. Didn’t we take IoU threshold as the threshold to determine recall when plotting the recall-IoU curve?

So, I read Hosang’s paper¹⁷ again, and I find that, “X” in “${\text{AR}}^{\text{max}=\text{X}}$ : AR given X (1/10/100) detection(s) per image” may represent the number of proposals.

From Ma’s paper¹⁹, “Object proposal aims to generate a certain amount of candidate bounding boxes to determine the potential objects and their locations in an image, which is widely applied to many visual tasks for pre-processing, e.g., object detection, segmentation, object discovery, and 3D match.” Therefore, I think that a candidate bounding box can be viewed as a proposal.

Although I haven’t conducted any specific target detection work, after searching some references, I guess that there exists a type of object detection neural network, may called Region Proposal Network (RPN)²⁰, which can generate multiple proposals with different scores for a single image. Therefore, if we calculate AR based on the proposal with the highest score for each image, then the AR metric in this case is so-called ${\text{AR}}^{\text{max}=\text{1}}$; similarly, if we calculate AR based on the proposals with the first 100 highest score for each image, then ${\text{AR}}^{\text{max}=\text{100}}$; and so on. It’s not hard to conclude that, if the RPN is not that bad, as X increases (corresponding to a stricter test for detectors), metric ${\text{AR}}^{\text{max}=\text{X}}$ usually has a tendency to increase, as shown as another figure in Hosang’s paper¹⁷:

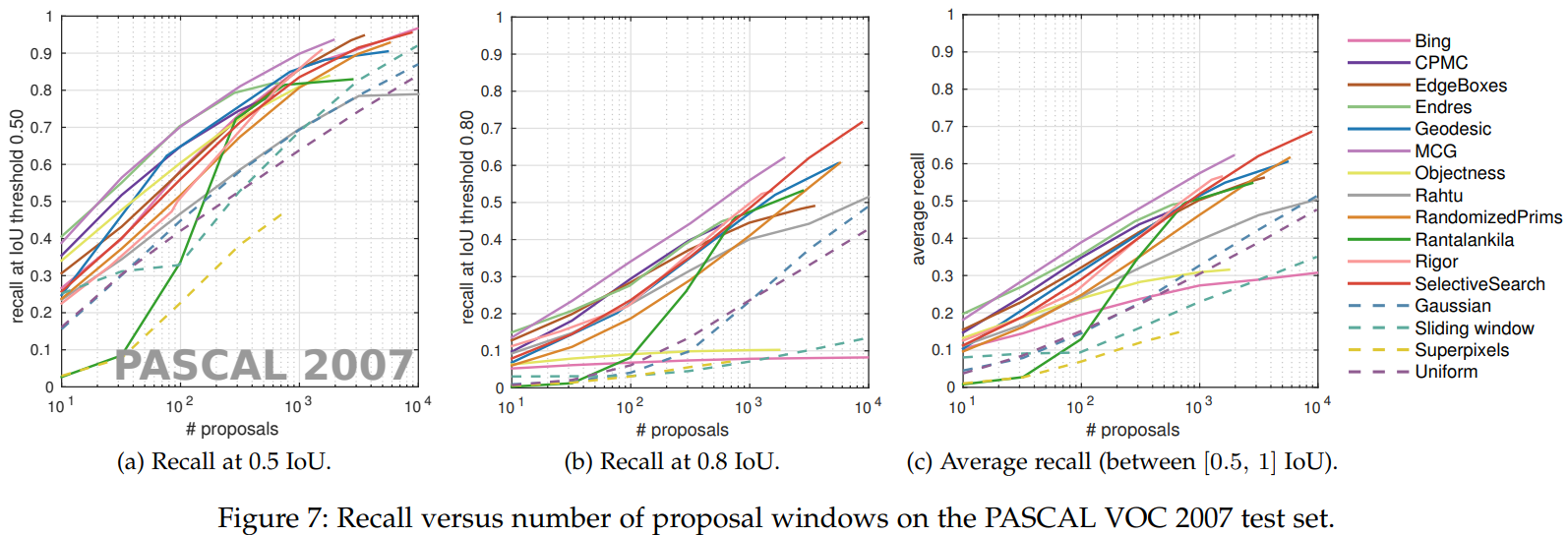
By the way …Permalink

The integration interval when calculating AP and ARPermalink

One thing that should be noted that, although theoretically, we can calculate the precision-recall/recall-IoU threshold curve across the interval of IoU threshold ranging from 0 to 1, in practice we usually choose the interval starting from 0.5 to calculate AP/AR, shown as Table I and Fig. 1, the example of calculating AP and that of AR.

About this point, a footnote in Hosang’s paper¹⁷ provides a fairly clear explanation; there is no need to discuss more:

mAP and mARPermalink

As mentioned before, many detectors could not only predict the positions of bounding boxes, but also the labels (categories) for objects in the boxes. Therefore, if we calculate APs/ARs for all categories, and then average their sum, we can obtain the metric Mean Average Precision (mAP)/Mean Average Recall (mAR).

That being said, the nuance between AP/AR and mAP/mAR would be deliberately neglected at times, like COCO detection challenge⁴¹³:

“AP is averaged over all categories. Traditionally, this is called “mean average precision” (mAP). We make no distinction between AP and mAP (and likewise AR and mAP) and assume the difference is clear from context.”

However, it doesn’t mean that AP for each category doesn’t matter. For example, Hosang’s paper¹⁷ made a detailed comparison and analysis for APs at category level:

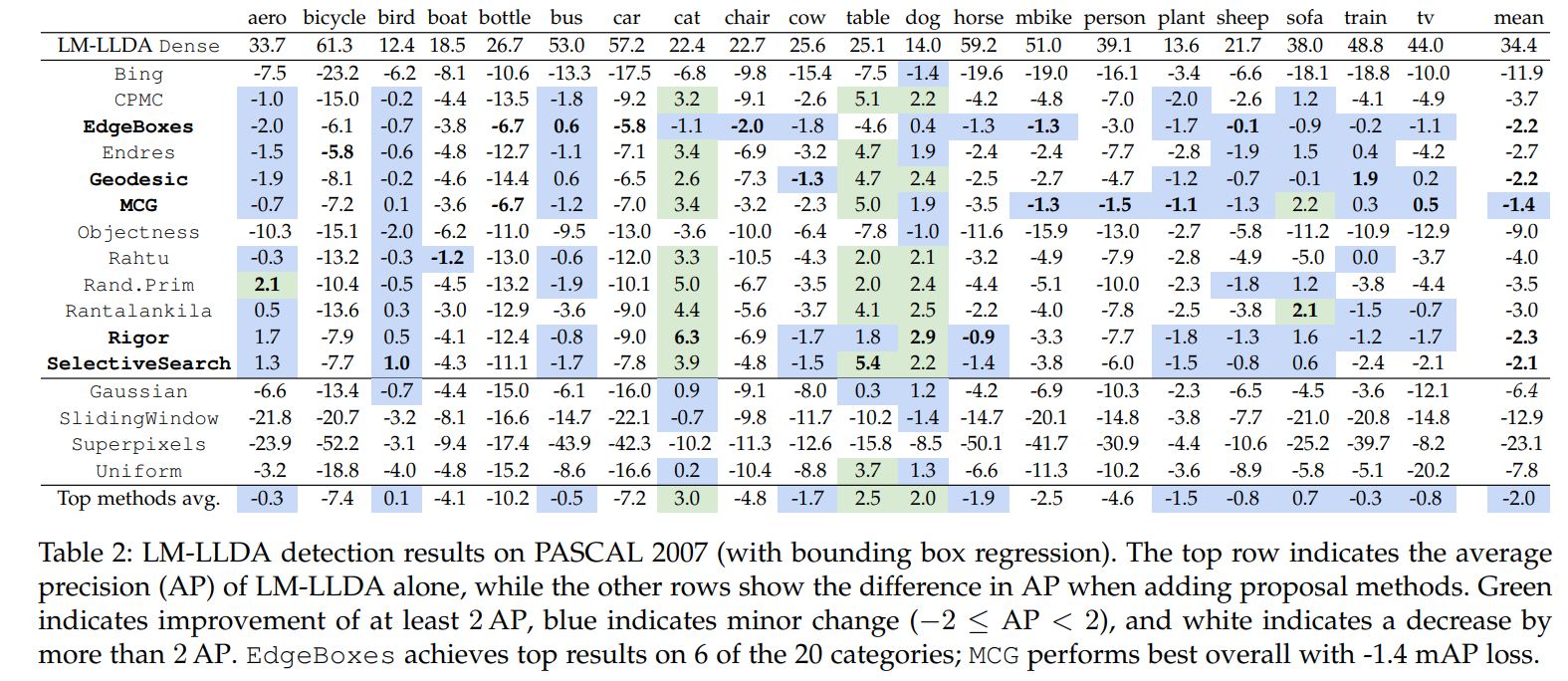
So, although COCO detection evaluation webpage¹³ says their code doesn’t emphasize the difference between AP and mAP, I think COCO API²¹ still supports computing and outputting AP for each category while evaluating detectors. I would verify this point further if I have the opportunity to deal with specific object detection task.

ReferencesPermalink