The Eigenvalue Interval Pattern of Random Hermitian Matrix
The eigenvalue interval pattern of random Hermitian matrix
随机矩阵是由随机选取的数所构成的矩阵(实际上由计算机所产生的都是伪随机)。假设现在有一个埃尔米特矩阵,并且其中的元素:
- 非主对角线的复数元素的所有实部和虚部都是标准正态分布随机数;
- 非主对角线上的实数都标准正态分布随机数的$\sqrt2$倍;
这样的矩阵被称作是随机埃尔米特矩阵,并且它本质上仍然满足埃尔米特矩阵的定义,因此它的本征值都是实数 [2]。
高阶的高斯随机埃尔米特矩阵被证明恰恰适合作为某种量子动态系统的行为模型:它的本征值与实验中观察到的能级非常相符。因此,随机埃尔米特矩阵的本征值成了20世纪60年代被深入研究的主题,尤其是它们的间隔非常令人感兴趣。它们的间隔并不是随机的。对于两个相同的能级来说,其间隔远比按随机方法所预期的不寻常。这就是所谓的排斥现象:能级之间努力尽可能原理,就像是不爱交往的人们所排成的一个长队。
例如,我们现在构造出一个269阶的随机埃尔米特矩阵,并将它们的本征值绘制出来:

它的本征值的范围是:$[-45.3140,45.3889]$。我们可以看到,这些间隔没有明显的模式,我们可能会认为它是随机的,但其实并非如此。
如果在相同的间隔(即$[-45.3140,45.3889]$)内完全随机地抽取269个数(服从均匀分布),并以相同的方式作图:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
clc,clear,close all
rng("default")
% Construct Hermitian matrix
order = 269;
A = randn(order);
HReal = tril(A,-1)+triu(A',0);
DiagCoeff = sqrt(2)*diag(ones(order,1));
DiagCoeff(DiagCoeff==0) = 1;
HReal = DiagCoeff.*HReal;
B = randn(order);
Hcomplex = tril(B,-1)-triu(B',0);
Hcomplex = (1-diag(ones(order,1))).*Hcomplex;
H = HReal+Hcomplex*1i;
EigValues = eig(H);
disp(min(EigValues))
disp(max(EigValues))
% Random ponits drawn from uniform distribution
RandomPoints = rand(1,order)*(max(EigValues)-min(EigValues))+min(EigValues);
RandomPoints = sort(RandomPoints);
figure('Units','pixels','Position',[71,482.33,2399.33,253.99])
hold(gca,'on')
box(gca,'on')
grid(gca,'on')
scatter(EigValues,2*ones(1,numel(EigValues)),10, ...
'filled','MarkerFaceColor',[7,84,213]/255, ...
'DisplayName','Eigenvalues of Hermitian matrix')
scatter(RandomPoints,ones(1,numel(RandomPoints)),10, ...
'filled','MarkerFaceColor',[249,82,107]/255,...
'DisplayName','Uniform distribution random points')
title(sprintf("std(diff(EigValues)) = %.4f, std(diff(RandomPoints)) = %.4f",std(diff(EigValues)), std(diff(RandomPoints))))
legend()
set(gca,'yticklabel',[])
xlim([-50,50])
ylim([0.5,2.5])
xlabel("Value")
exportgraphics(gcf,"fig-1.jpg","Resolution",600)
figure
hold(gca,'on')
box(gca,'on')
grid(gca,'on')
bins = 100;
histogram(EigValues,bins,"FaceColor",[7,84,213]/255,"DisplayName","Eigenvalues of Hermitian matrix")
histogram(RandomPoints,bins,"FaceColor",[249,82,107]/255,"DisplayName","Uniform distribution random points")
legend();
ylabel("Frequency")
xlabel("Value")
exportgraphics(gcf,"fig-2.jpg","Resolution",600)

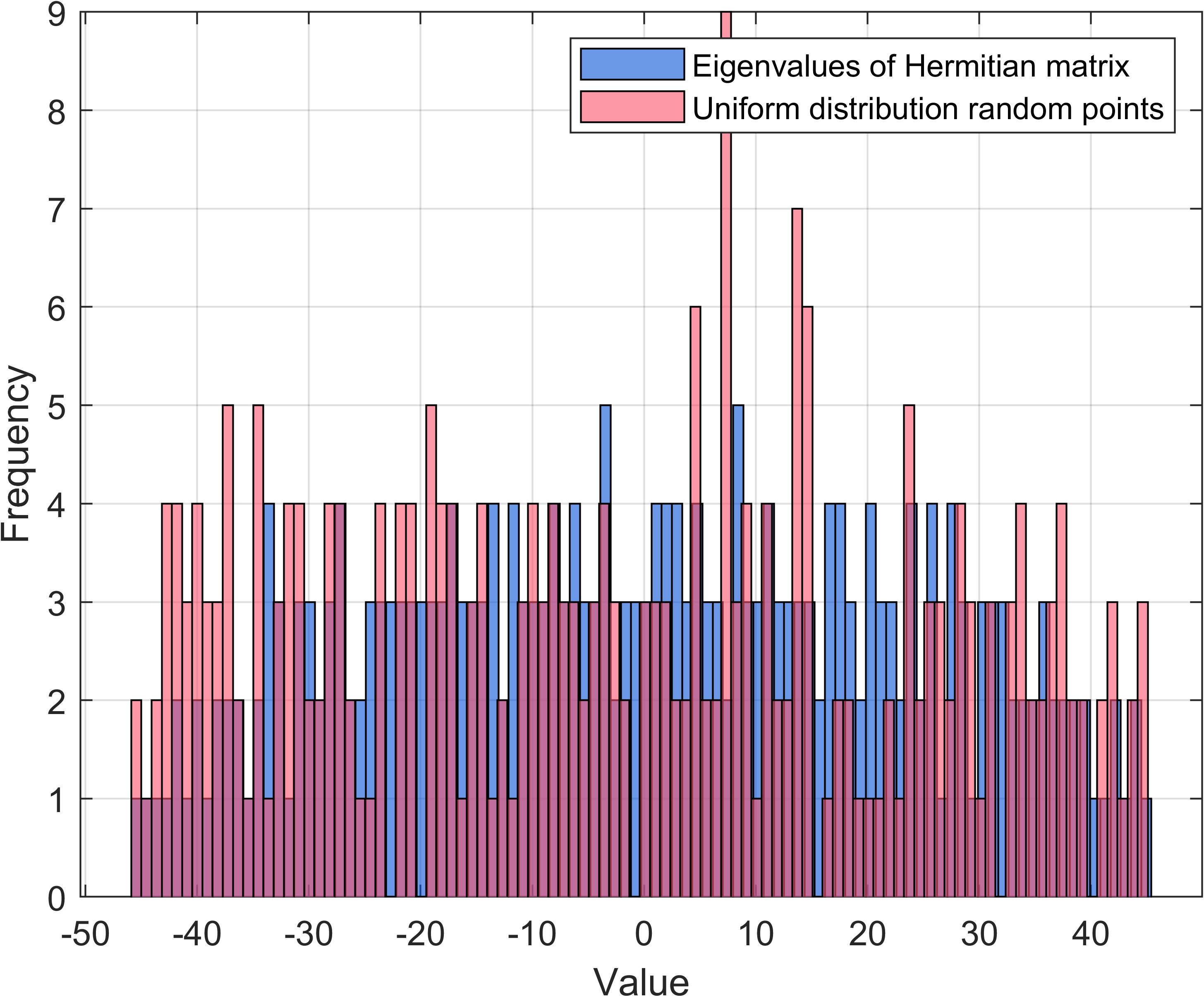
我们可以明显地看到随机埃尔米特矩阵本征值之间的排斥效应:产生自均匀分布的随机数中所具有的非常接近的相邻数对比本征值分布中的相邻数对更多,并且数对之间离得也更远。
并且由于实对称矩阵是一种特殊的埃尔米特矩阵,因此对于随机实对称阵 [2],同样具有类似的排斥效应:
因此,尽管本征值之间并不想形成任何可辨认的模式(因为它们毕竟是从一个随机矩阵中计算产生的),但是却尽力保持着互相之间的距离。与此形成鲜明对比的是,一个纯粹的随机点如果发现自己同另一个随机点挤在一起,它似乎根本不会在乎。
-
像这样的高斯随机埃尔米特矩阵的集合,在总体上称为高斯幺正系综(Gaussian Unitary Ensemble),简称为GUE(念作“goo”);
注:这里真正想讨论的是算子。算子为描述动态系统提供了一个数学模型。“系综”这个词的用法源于爱因斯坦,指的是那些具有共同统计性质的算子的集合。
-
像随机埃尔米特矩阵本征值所表现出的那一长串非均匀分布的数之间的间隔,其精确的统计性质被概括称为对关联函数(pair correlation function);
-
与对关联函数,以及它极其与众不同的特征有关的某种比率,被称为它的形状因子(form factor)。
Something else …
2023年5月6日
今天突然觉得埃尔米特矩阵的特征值的分布看起来像个拥挤但是又有秩序的队列,会不会和排队论有些关系呢?
References
[1] Derbyshire J. Prime obsession: Bernhard Riemann and the greatest unsolved problem in mathematics[M]. Joseph Henry Press, 2003.

