Introduction

本文对于连续性和参数化的讨论均来自密西根科技大学(Michigan Technological University, MTU)信息技术官方网站，原文可见：Michigan Technological University Informative Technology: Continuity Issues.

正如在B-rep中提到的，一个固体的edges和faces可以使用curve segments和surface patches进行表示，而不是使用简单的line segments和polygons。但是，这种方式也会产生一些问题。

B-rep(AKA Boundary representation): Boundary representation - Wikipedia.

In solid modeling and computer-aided design, boundary representation (often abbreviated B-rep or BREP) is a method for representing a 3D shape by defining the limits of its volume. A solid is represented as a collection of connected surface elements, which define the boundary between interior and exterior points.

比如，在下面的图像中，我们将三个BREP curvilinear patches连接到一起。

两个曲线边界分别使用黄色和白色表示，并且两条曲线在顶点$X$处交汇。记这两条曲线分别为$f(u)$和$g(v)$，其中$u$和$v$分别从区间$[a, b]$和$[m, n]$取值。问题在于，我们如何保证这些区间以平滑的方式连接在一起呢？(How we can make sure that these curves join together in a “smooth” way.)

考虑曲线$f()$的右端点$f(b)$和曲线$g()$的左端点$g(m)$。

• 如果$f(b)$和$g(m)$值相等(如上图所示)，那么就称曲线$f()$和$g()$在点$f(b)=g(m)$处$\boldsymbol{C^0}$ continuous；
• 如果对于$i\le k$，曲线$f()$和$g()$的第$i$阶导数值在点$f(b)=g(m)$处都是相等的，那么我们称两条曲线是$\boldsymbol{C^k}$ continuous；
• 如果在连接点处，两条曲线的曲率(curvatures)是相同的，那么称两条曲线在连接点处是curvature continuous；

直观上看，两条曲线是$\boldsymbol{C^0}$ continuous，则表明我们可以从一条曲线走到另一条曲线是不需要经过一个gap；两条曲线是$\boldsymbol{C^1}$ continuous，表明从一条曲线走到另一条曲线经过连接点处的速度是相同的；两条曲线是$\boldsymbol{C^2}$ continuous，则表明在连接点处除了速度是相同的以外，加速度也是相同的。因此在连接点处，$\boldsymbol{C^2}$ continuous比$\boldsymbol{C^1}$ continuous更加平滑，$\boldsymbol{C^1}$ continuous比$\boldsymbol{C^0}$ continuous更加平滑。

两条曲线是curvature continuous，则表明在连接点处turning rate是相同的；然而，此时在连接点处的二阶导数可能是不相同的。也就是说，curvature continuous不能够保证$\boldsymbol{C^2}$ continuous；但是，$\boldsymbol{C^2}$ continuous可以保证curvature continuous，这一点可以由曲率的计算公式得到。

从连续性的定义可以得到，如果在连接点$f(b)=g(m)$处，两条曲线是$\boldsymbol{C^k}$ continuous，那么对于所有的$i\le k$都是$\boldsymbol{C^i}$ continuous；如果在连接点处$\boldsymbol{C^k}$ continuous是无法保证的，那么对于任意的$i\ge k$，都不可能是$\boldsymbol{C^i}$ continuous。

Problems with Parametric Representations

到目前为止，$\boldsymbol{C^k}$ continuous看起来是个完美的用于描述两条曲线连接平滑程度的概念。但是，它确实存在一定的问题。

考虑以下两个用参数方程表示的直线片段：

其中，点A，B和C是三个在同一条直线上的点，如下图所示。

随着变量$u$(或者$v$)从0变化到1，则$f(u)$(或者$g(v)$)从点A运动到点B(从点B运动到点C)。我们很容易看到，直线AB和直线BC在B点是$\boldsymbol{C^0}$ continuous，但是它们在B点是$\boldsymbol{C^1}$ continuous吗？

对式$\eqref{eq1}$两边求导，可以得到：

两者并不是相等的，因此线段AB和BC在点B处并不是$\boldsymbol{C^1}$ continuous。

这一点很奇怪，因为从直观上看，这两条曲线的连接是非常平滑的，甚至可以当做是一条直线。那么问题出在哪里呢？

其实这个问题就是由参数化(parameterization)所导致的。如果我们将方向向量$B-A$和$C-B$用单位长度向量代替，并且改变参数$u$和$v$的参数域，这样的问题将会消失。也就是说，将公式$\eqref{eq1}$改为以下的形式：

其中，$u$从0到$\vert B-A\vert$变化，而$v$从0到$\vert C-B\vert$变化。此时对公式$\eqref{eq3}$两端求导，可以得到：

即$F’(u)=G’(v)$，且都等于从点A指向点C的unit-length vector，这样两条线段就是$\boldsymbol{C^1}$ continuous。因此，曲线的重新参数化(reparameterizing)能够解决这个问题。

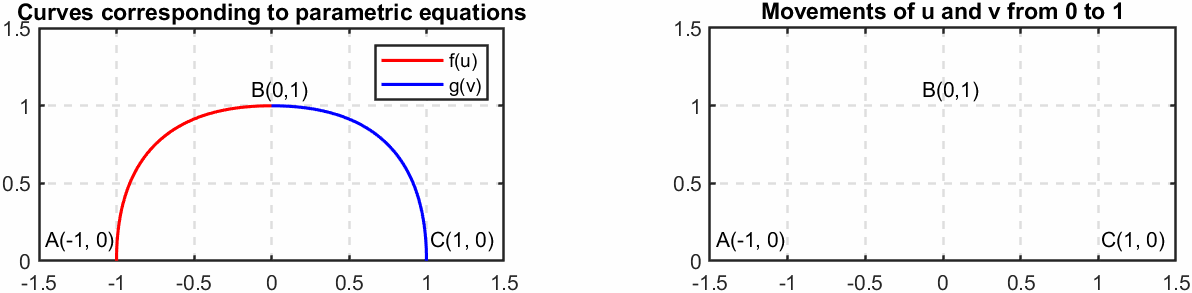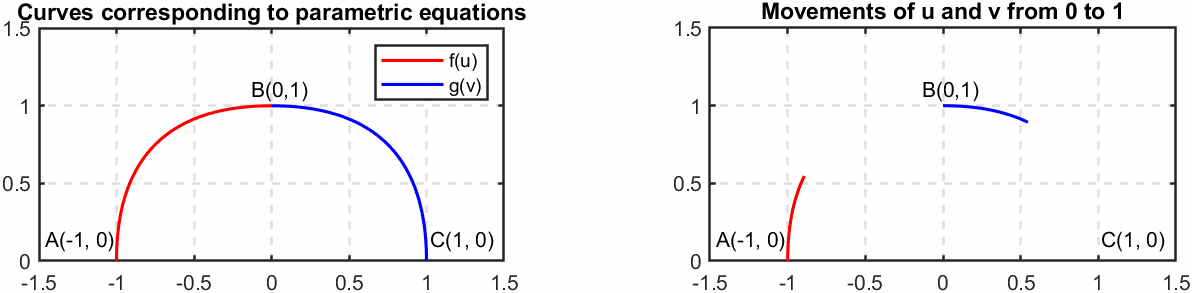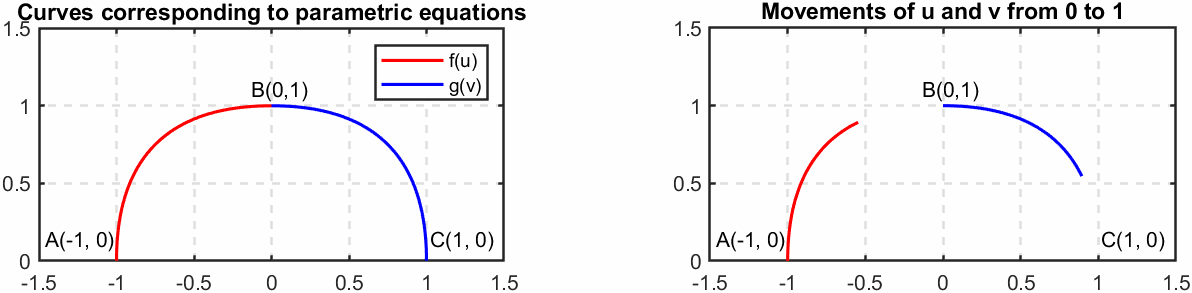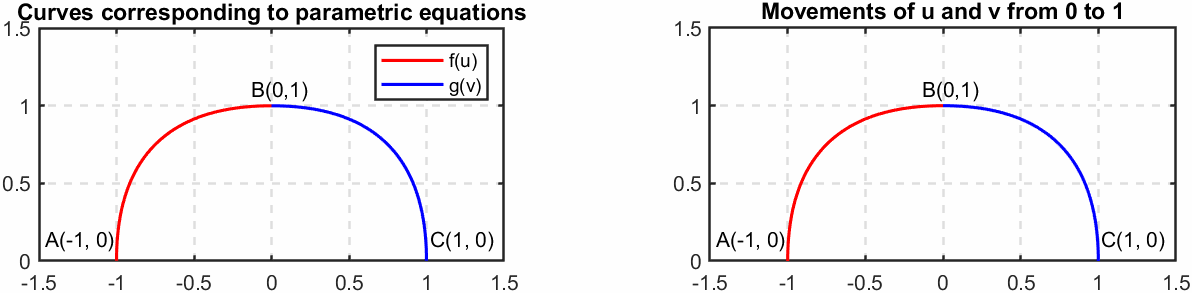
我们可以看一个例子。对于两条曲线：

两个参数方程所对应的曲线以及运动轨迹如下图所示：

（上图使用MATLAB软件绘制，具体代码见文末的Appendix A）

两条曲线的连接点是点B。对于式$\eqref{eq5}$两端求导(向量对标量求导)，可以得到：

在连接点B处，我们可以得到：

可以看出：

注意到，$g’(0)$和$g’‘(0)$都是零向量，没有很好地定义。因此，我们无法讨论连接点处的连续性；但是，根据图像我们可以看到，两条曲线“看起来”有一些连续的性质，因为至少在连接点处它们有共同的切线。

接下来，我们对这些曲线进行reparameterization，即只改变它们的参数方程，而不改变曲线的形状。

在式$\eqref{eq5}$中，令$u^2=p$，$v^2=q$，得到新的参数方程：

对上式求一阶导数和二阶导数：

进一步得到：

即：

因此，在更改变量后，我们可以看到，这两条曲线实际上是$\boldsymbol{C^1}$ continuous和$\boldsymbol{C^2}$ continuous。并且还可以验证，它们是curvature continuous，因为它们的曲率处处为1。因此，reparameterization或者change of variable对于连续性有dramatic impact。

Arc Length Parameterization

从上面我们可以看到，同一条曲线的不同参数化形式会得到不同的连续性结论。人们可能会问：是否有一种参数化形式，使得我们能够相信由它推导出的连续性结果？(Is there a parameterization that we can trust for continuity discussion?)幸运的是，答案是肯定的，数学家们早就解决了这个问题。这个trick是使用arc length作为参数。

令curve segment的长度为$s$，我们可以用$f(u)$参数化这条曲线，$u$表示曲线上的点到初始点$f(0)$的距离，其中$u$从0取到$s$。通过这种arc length参数化的方式，随着$u$从0移动到$s$，$f(u)$以相同的速度从曲线的$f(0)$移动$f(s)$。因此，衡量速度的tangent vector就是unit-length。不仅如此，很多公式都能得到简化。

那么，为什么我们不使用arc length parameterization来简化计算呢？答案也非常简单。尽管arc length parameterization非常简单，并且在理论上是elegant，但是它的计算繁琐，不切实际。人们可以很容易地在一些方便地参数化中设计曲线，但是有时候用arc length重新参数化是极其困难的。也就是说，找到arc length并不是一件简单的事情，因为这涉及到包含平方根的函数进行积分。比如说，椭圆这个看起来很简单的图形，它的周长没有解析解，需要用到椭圆积分。

因此，即使non-arc length的参数化方式会导致一些问题，我们也不会使用arc length参数化的方式。

Geometric Continuity

我们上面提到说，$\boldsymbol{C^2}$ continuous可以保证curvature continuous，但是curvature continuous不能够保证$\boldsymbol{C^2}$ continuous。事实上，许多$\boldsymbol{C^1}$ continuous并且curvature continuous的曲线并不满足$\boldsymbol{C^2}$ continuous，甚至这些曲线中的许多曲线甚至不是二阶可导的。这些曲线在连接点处看起来是很平滑的，并且在从一条曲线过渡到另一条曲线时(movement)也是很平滑的，甚至其中的一些曲线在更改变量后，可以在连接点处做到$\boldsymbol{C^2}$ continuous。但是，能够做到这一点的reparameterization方法事实上时非常难找到的。因此，我们会放松$\boldsymbol{C^2}$ continuous的要求：

$\boldsymbol{G^k}$ continuous

Two curve segments are said $\boldsymbol{G^k}$ geometric continuous at the joining point if and only if all i-th derivatives, i less than or equal to k, computed with arc length parameters agree at the joining point.

在定义中，我们使用了arc length。但是，arc length parameterization并不是必要的，我们可以使用另一个等价形式的定义：

$\boldsymbol{G^k}$ continuous(equivalent definition without arc length parameterization)

Two curve segments are said $\boldsymbol{G^k}$ geometric continuous at the joining point if and only if there exists two parameterizations, one for each curve segment, such that all i-th derivatives, i less than or equal to k, computed with these new parameterizations agree at the joining point.

这个定义稍微简单一些，但仍然不够好，因为实际上我们不知道如何找到这样的参数化方式。但是，当$k=1$和$k=2$时非常简单。对于$k=1$的情形：

Two $\boldsymbol{C^0}$ curve segments are said $\boldsymbol{G^1}$ geometric continuous at the joining point if and only if vectors $f’(u)$ and $g’(v)$ are in the same direction at the joining point.(Note that $f’(u)$ and $g’(v) $are evaluated at the joining point.)

因为如果在连接点处的tangent vectors相同(即有相同的方向)，那么两条曲线在连接点处就有相同的tangent line。但是注意，反之并不成立。准确讲，有相同tangent line的两个curve segments并不意味着在连接点它们是$\boldsymbol{G^1}$ continuous。比如在下图中：

曲线$f(u)$和$g(v)$在连接点处有着相同的tangent line，但是连接点处的tangent vectors的方向是相反的，因此在连接点处就不是$\boldsymbol{G^1}$ continuous。

G. Neilson 发现了一个非常简单的公式用于定义$\boldsymbol{G^2}$ continuous：

Two $\boldsymbol{C^1}$ curve segments are said $\boldsymbol{G^2}$ geometric continuous at the joining point if and only if vector $f’‘(u) - g’‘(v)$ is parallel to the tangent vector at the joining point.(Note that $f’‘(u)$ and $g’‘(v)$ are evaluated at the joining point.)

$\boldsymbol{G^2}$ continuity这一特性的优点在于它适用于任何参数化方式。但是我们需要注意，我们首先需要保证$C^1$ continuity条件。

我们使用一个例子说明Neilson的发现。

考虑下面两个抛物线片段，它们的的连接点是$(0,1,0)$：

它们的图像以及运动轨迹如下图所示：

(MATLAB绘图代码见文末的Appendix B)

对式$\eqref{eq6}$求导，可以得到：

进一步得到：

此时可以看出$\boldsymbol{C^1}$ continuous，但是并不满足$\boldsymbol{C^2}$ continuous。但是有：

即$f’‘(1)-g’‘(0)$与$f’(1)$和$g’(0)$平行，因此这个这两条曲线在连接点处是$\boldsymbol{G^2}$ continuous。并且可以计算得到，这两条曲线是curvature continuous。

Appendix

Appendix A

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
clc, clear, close all

u = linspace(0, 1, 50);
v = linspace(0, 1, 50);

f = [-cos(pi/2*u.^2); sin(pi/2*v.^2)];
g = [sin(pi/2*u.^2); cos(pi/2*v.^2)];

figure("Units", "pixels", "Position", [420, 334, 939, 502])
tiledlayout(1, 2)
axislimits = [-1.5, 1.5, 0, 1.5];
LineWidth = 1.5;
FontSize = 10;

nexttile
hold(gca, "on")
grid(gca, "on")
box(gca, "on")
axis(gca, "equal")
axis(axislimits)
set(gca, 'PlotBoxAspectRatio', [1 1 1])
ax = gca;
ax.GridLineStyle = '--';
ax.LineWidth = 1.2;
title("Curves corresponding to parametric equations")
text(-0.1342, 1.1074, 'B(0,1)', FontSize=FontSize)
text(-1.4630, 0.1409, 'A(-1, 0)', FontSize=FontSize)
text(1.0201, 0.1409, 'C(1, 0)', FontSize=FontSize)
plot(f(1, :), f(2, :), LineWidth=LineWidth, Color='r')
plot(g(1, :), g(2, :), LineWidth=LineWidth, Color='b')
legend("f(u)", "g(v)")

nexttile
hold(gca, "on")
grid(gca, "on")
box(gca, "on")
axis(gca, "equal")
axis(axislimits)
set(gca, 'PlotBoxAspectRatio', [1 1 1])
ax = gca;
ax.GridLineStyle = '--';
ax.LineWidth = 1.2;
text(-0.1342, 1.1074, 'B(0,1)', FontSize=FontSize)
text(-1.4630, 0.1409, 'A(-1, 0)', FontSize=FontSize)
text(1.0201, 0.1409, 'C(1, 0)', FontSize=FontSize)
title("Movements of u and v from 0 to 1")
h1 = animatedline(LineWidth=1.5, Color='r');
h2 = animatedline(LineWidth=1.5, Color='b');
for i = 1:width(u)
    addpoints(h1, f(1, i), f(2, i))
    addpoints(h2, g(1, i), g(2, i))
    drawnow
    pause(0.05)
    exportgraphics(gcf, "gif.gif","Append", true)
end

Appendix B

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
clc, clear, close all

clc, clear, close all

u = linspace(0, 1, 50);
v = linspace(0, 1, 50);

f = [-1+u.^2; 2*u-u.^2];
g = [2*u-u.^2; 1-u.^2];

figure("Units", "pixels", "Position", [420, 334, 939, 502])
tiledlayout(1, 2)
axislimits = [-1.5, 1.5, 0, 1.5];
LineWidth = 1.5;
FontSize = 10;

nexttile
hold(gca, "on")
grid(gca, "on")
box(gca, "on")
axis(gca, "equal")
axis(axislimits)
set(gca, 'PlotBoxAspectRatio', [1 1 1])
ax = gca;
ax.GridLineStyle = '--';
ax.LineWidth = 1.2;
title("Curves corresponding to parametric equations")
text(-0.1342, 1.1074, 'B(0,1)', FontSize=FontSize)
text(-1.4630, 0.1409, 'A(-1, 0)', FontSize=FontSize)
text(1.0201, 0.1409, 'C(1, 0)', FontSize=FontSize)
plot(f(1, :), f(2, :), LineWidth=LineWidth, Color='r')
plot(g(1, :), g(2, :), LineWidth=LineWidth, Color='b')
legend("f(u)", "g(v)")

nexttile
hold(gca, "on")
grid(gca, "on")
box(gca, "on")
axis(gca, "equal")
axis(axislimits)
set(gca, 'PlotBoxAspectRatio', [1 1 1])
ax = gca;
ax.GridLineStyle = '--';
ax.LineWidth = 1.2;
text(-0.1342, 1.1074, 'B(0,1)', FontSize=FontSize)
text(-1.4630, 0.1409, 'A(-1, 0)', FontSize=FontSize)
text(1.0201, 0.1409, 'C(1, 0)', FontSize=FontSize)
title("Movements of u and v from 0 to 1")
h1 = animatedline(LineWidth=1.5, Color='r');
h2 = animatedline(LineWidth=1.5, Color='b');
for i = 1:width(u)
    addpoints(h1, f(1, i), f(2, i))
    addpoints(h2, g(1, i), g(2, i))
    drawnow
    pause(0.05)
    exportgraphics(gcf, "gif1.gif","Append", true)
end